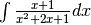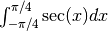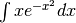Sage як калькулятор¶
У цій частині підручника ми розглядаємо команди, які дозволяють використовувати Sage як графічний калькулятор. Розділи про арифметичні операції та функції, а також про розв’язування рівнянь та нерівностей становлять основу для подальшого матеріалу. Розділи із побудови графіків, математичної статистики та математичного аналізу не залежать один від одного, але може бути доцільним пройти навчальний матеріал щодо побудови графіків раніше, оскільки цей інструментарій візуалізації результатів інтенсивно використовується як у статистиці, так і в матаналізі.
Арифметичні дії та функції¶
Основні арифметичні дії¶
До основних арифметичних операцій відносяться +, -, * та /, що позначають відповідно додавання, віднімання, множення та ділення. Операція ^ позначає піднесення до ступеня.
sage: 1+1
2
sage: 103-101
2
sage: 7*9
63
sage: 7337/11
667
sage: 11/4
11/4
sage: 2^5
32
Символ - перед числом вказує на його від’ємний знак.
sage: -6
-6
sage: -11+9
-2
Не дивно, що Sage дотримується стандартного порядку операцій, який у англомовній літературі позначають “PEMDAS” (Parenthesis - дужки, Exponents - піднесення до ступеня, Multiplication - множення, Division - ділення, Addition - додавання, Substraction - віднімання)
sage: 2*4^2+1
33
sage: (2*4)^2+1
65
sage: 2*4^(2+1)
128
sage: -3^2
-9
sage: (-3)^2
9
При діленні двох цілих чисел виникає певна неоднозначність: чи результатом буде дріб, чи його наближене десяткове представлення. На відміну від більшості графічних калькуляторів, Sage намагається дати найбільш точний результат, наскільки це можливо. Тому якщо не вказано інше, повертає дріб. Для виведення результату саме у десятковій формі можна включити точку у вихідний вираз.
sage: 11/4.0
2.75000000000000
sage: 11/4.
2.75000000000000
sage: 11.0/4
2.75000000000000
sage: 11/4*1.
2.75000000000000
Вправи:
Розділити
на
у п’ятому ступені, подати результат у вигляді раціонального числа, потім представити його наближення у десятковому вигляді.
Знайти десяткове представлення виразу
Обчислити у Sage вираз
(-9)^(1/2). Описати результат.
Integer Division and Factoring¶
Необхідно знати розділ “Основні арифметичні дії“
Буває так, що оператор ділення не дає нам усієї необхідної інформації. Часто нам треба знати не тільки зведений дріб або його приблизне значення у десятковому записі, але частку і залишок як результати операції ділення.
Для обчислення частки використовуємо оператор //, а для отримання залишку - оператор %.
sage: 14 // 4
3
sage: 14 % 4
2
Якщо треба отримати і частку, і залишок, скористаємося командою divmod()
sage: divmod(14,4)
(3, 2)
Пригадаймо, що 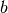 є дільником
є дільником  , якщо залишок від ділення цих двох цілих чисел дорівнює нулю. Серед операцій із цілими числами у Sage є вбудована команда (або “метод”), що дозволяє перевірити, чи подільні два цілі числа.
, якщо залишок від ділення цих двох цілих чисел дорівнює нулю. Серед операцій із цілими числами у Sage є вбудована команда (або “метод”), що дозволяє перевірити, чи подільні два цілі числа.
sage: 3.divides(15)
True
sage: 5.divides(17)
False
Існує також споріднений до цієї команди метод divisors(). Цей метод повертає список усіх додатних дільників вказаного цілого числа.
sage: 12.divisors()
[1, 2, 3, 4, 6, 12]
sage: 101.divisors()
[1,101]
Якщо єдиними дільниками цілого числа є 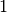 і саме це число, тоді ми називаємо таке число простим. Для перевірки, чи є дане число простим, у Sage можна використати метод
і саме це число, тоді ми називаємо таке число простим. Для перевірки, чи є дане число простим, у Sage можна використати метод is_prime().
sage: (2^19-1).is_prime()
True
sage: 153.is_prime()
False
Зауважте, що у першому прикладі 2^19 -1 стоїть у дужках. Ці дужки істотні для визначення порядку операцій у Sage, і без них результат може бути зовсім іншим. Спробуйте обчислити вираз 2^19-1.is_prime() і порівняйте результат. Якщо є сумніви щодо порядку дій у виразі, краще використовувати дужки.
Метод factor() служить для розбиття цілого числа на добуток простих множників.
sage: 62.factor()
2 * 31
sage: 63.factor()
3^2 * 7
If we are interested in simply knowing which prime numbers divide an integer, we may use it’s prime_divisors() (or prime_factors()) method.
sage: 24.prime_divisors()
[2, 3]
sage: 63.prime_factors()
[3, 7]
І нарешті, пригадаймо поняття про найбільший спільний дільник та найменше спільне кратне двох цілих чисел. Спільний дільник - це будь-яке ціле число, на яке ділиться кожне з двох чисел без залишку, а спільне кратне - це число, яке ділиться без залишку на обидва ці числа.
Найбільший спільний дільник (gcd), що не дивно, є найбільшим з множини цих спільних дільників. Він обчислюється за допомогою команди gcd().
sage: gcd(14,63)
7
sage: gcd(15,19)
1
Якщо два числа не мають нетривіальних спільних дільників, тоді вважається, що результат знаходження gcd є 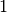 .
.
Найменше спільне кратне двох чисел є найменшим з чисел, що їх ділять без залишку ці два числа. Воно обчислюється командою lcm().
sage: lcm(4,5)
20
sage: lcm(14,21)
42
Вправи:
Знайдіть частку і залишок при діленні
на
.
За допомогою Sage перевірте, чи знайдені частка і залишок правильні.
Перевірте, чи буде
дільником
.
- Compute the list of divisors for each of the integers
and
.
Які з цих чисел є простими?
Обчисліть
,
та
для пар цілих чисел
та
. Як співвідносяться між собою gcd, lcm та добуток двох чисел?
Стандартні функції і сталі¶
Sage містить майже усі стандартні функції, які можуть зустрітися при вивченні математичної дисципліни. У цьому розділі ми розглянемо найчастіше вживані функції: максимум, мінімум, округлення вниз та вгору, тригонометричні, експоненціальні та логарифмічні функції. Також буде розглянуто деякі стандартні математичні константи, такі, як стала Ейлера ( ),
), 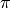 , і золоте відношення (
, і золоте відношення (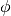 ).
).
Команди max() та min() дають найбільше та найменше з деякого набору чисел.
sage: max(1,5,8)
8
sage: min(1/2,1/3)
1/3
Для цих функцій можна задавати довільну кількість аргументів.
Команда abs() у Sage дозволяє обчислити абсолютне значення дійсного числа.
sage: abs(-10)
10
sage: abs(4)
4
Команда floor`дає заокруглення до найближчого цілого числа знизу, а :func:().ceil` - до найближчого цілого згори.
sage: floor(2.1)
2
sage: ceil(2.1)
3
При використанні команд floor() та ceil() слід бути уважним:
sage: floor(1/(2.1-2))
9
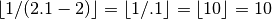 . Це очевидно невірний результат. Що ж трапилось?
. Це очевидно невірний результат. Що ж трапилось?
sage: 1/(2.1-2)
9.99999999999999
Дійсні числа зберігаються у пам’яті комп’ютера у двійковому форматі, тоді як для нас звичним є десяткове представлення. Вираз 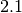 у десятковому записі виглядає просто і компактно, але перетворення його до двійкового запису дає
у десятковому записі виглядає просто і компактно, але перетворення його до двійкового запису дає 
Комп’ютер не може зберігати нескінченну кількість цифр, і тому такий вираз заокруглюється на якійсь довжині, що дає невелику похибку заокруглення, яку ми і побачили. Але у Sage представлення раціональних чисел (дробей) є точним, тому тут помилки заокруглення не виникає.
sage: floor(1/(21/10-2))
10
Тому у багатьох випадках може бути кращим використовувати за можливості раціональі числа замість десяткових, особливо якщо вимагається підвищена точність обчислень.
Команда sqrt() дає квадратний корінь дійсного числа. Так само як у випадку дробів, отримати десяткове наближення результату можна, якщо задати вихідний аргумент у десятковому вигляді.
sage: sqrt(3)
sqrt(3)
sage: sqrt(3.0)
1.73205080756888
Для знаходження інших коренів використовується експонента із раціональним показником. Sage може обчислити результат піднесення до будь-якого раціонального ступеня. Якщо експонента або основа є десятковим числом, результат також є десятковим.
sage: 3^(1/2)
sqrt(3)
sage: (3.0)^(1/2)
1.73205080756888
sage: 8^(1/2)
2*sqrt(2)
sage: 8^(1/3)
2
Sage також має набір усіх стандартних тригонометричних функцій: так, синус та косинис обчислюються відповідно за допомогою команд sin() та cos().
sage: sin(1)
sin(1)
sage: sin(1.0)
0.841470984807897
sage: cos(3/2)
cos(3/2)
sage: cos(3/2.0)
0.0707372016677029
Тут поведінка програми аналогічна поведінці, яку ми розглянули на прикладі операції sqrt(): Sage обчислює точний результат. На перший погляд тут немає місця неоднозначності, оскільки неможливо далі спростити вираз, скажімо, sin(1). Проте деякі вирази із синусом все ж таки підлягають спрощенню. Наприклад, ми маємо важливу геометричну тотожніість: 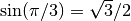 . У Sage є вбудоване символьне представлення числа
. У Sage є вбудоване символьне представлення числа 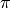 , і подібні тотожності відповідно є цілком зрозумілими програмі.
, і подібні тотожності відповідно є цілком зрозумілими програмі.
sage: pi
pi
sage: sin(pi/3)
1/2*sqrt(3)
При наборі pi у Sage мова йде саме про символьне значення 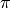 , а не про чисельне його наближення. Але також при необхідності можна звернутися до чисельного наближення за допомогою методу
, а не про чисельне його наближення. Але також при необхідності можна звернутися до чисельного наближення за допомогою методу n()
sage: pi.n()
3.14159265358979
sage: sin(pi)
0
sage: sin(pi.n())
1.22464679914735e-16
Таким чином, якщо використовується символьний об’єкт pi, Sage дає точний результат. Але якщо у аргументі використовується наближенне значення, ми відповідно отримуємо наближенний результат. Запис e-15 є короткою формою запису числа 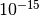 , а число
, а число 1.22464679914735e-16 має дорівнювати нулеві, але у результати вносяться похибки внаслідок використання наближень. Нижче наведено кілька прикладів порівняння використання символьного (точного) значення 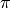 та його чисельного наближення:
та його чисельного наближення:
sage: sin(pi/6)
1/2
sage: sin(pi.n()/6)
0.500000000000000
sage: sin(pi/4)
1/2*sqrt(2)
sage: sin(pi.n()/4)
0.707106781186547
Слід додати до цього, що існують і менш відомі значення кутів, для яких можна провести елегантне спрощення виразів із синусом та косинусом.
sage: sin(pi/10)
1/4*sqrt(5) - 1/4
sage: cos(pi/5)
1/4*sqrt(5) + 1/4
sage: sin(5*pi/12)
1/12*(sqrt(3) + 3)*sqrt(6)
Аналогічно можна використовувати інші тригонометричні, а також обернені тригонометричні і гіперболічні функції.
sage: arctan(1.0)
0.785398163397448
sage: sinh(9.0)
4051.54190208279
Подібно до pi у Sage є вбудована символьна кнстанта для представлення числа  - основи натуральних логарифмів.
- основи натуральних логарифмів.
sage: e
e
sage: e.n()
2.71828182845905
Хоча часто використованою формою математичного запису є ln(x) для натуральних логарифмів і log(x) - для десяткових із основою 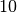 , у Sage обидві форми запису позначають логарифми із основою
, у Sage обидві форми запису позначають логарифми із основою  . Для використання іншої основи можна додати другий аргумент до відповідної команди: так, команда Sage
. Для використання іншої основи можна додати другий аргумент до відповідної команди: так, команда Sage log(x,b) використовується для обчислення 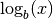 .
.
sage: ln(e)
1
sage: log(e)
1
sage: log(e^2)
2
sage: log(10)
log(10)
sage: log(10.0)
2.30258509299405
sage: log(100,10)
2
Потенціювання (обчислення піднесення  до ступеня) можна задати як за допомогою функції
до ступеня) можна задати як за допомогою функції exp():, так і підносячи символьну константу e до відповідного ступеня.
sage: exp(2)
e^2
sage: exp(2.0)
7.38905609893065
sage: exp(log(pi))
pi
sage: e^(log(2))
2
Вправи:
Обчисліть верхню і нижню цілі частини від
.
Обчисліть логарифм із основою
від
, потім - логарифм із основою 10 від
, обчисліть їх відношення. Яка має бути відповідь?
Обчисліть логарифм із основою 2 від
.
Порівняйте
із чисельним наближенням за допомогою
pi.n().Обчисліть
,
та
.
Розв’язування рівнянь і нерівностей¶
Розв’язування відносно x¶
Необхідно знати розділи “Основні арифметичні дії” та “Стандартні функції і сталі“
У Sage операції рівності і нерівності визначаються за допомогою операторів ==, <= та >=, а їх результатом є значення True, False, або, якщо аргументом є змінна, просто відповідна рівність або нерівність.
sage: 9 == 9
True
sage: 9 <= 10
True
sage: 3*x - 10 == 5
3*x - 10 == 5
Для розв’язку рівняння або нерівності використовується команда із влучною назвою solve(). Наразі ми будемо розв’язувати ці вирази лише щодо 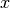 . У розділі про змінні показано, як використовувати інші змінні.
. У розділі про змінні показано, як використовувати інші змінні.
sage: solve(3*x - 2 == 5,x)
[x == (7/3)]
sage: solve( 2*x -5 == 1, x)
[x == 3]
sage: solve( 2*x - 5 >= 17,x)
[[x >= 11]]
sage: solve( 3*x -2 > 5, x)
[[x > (7/3)]]
Рівняння може мати кілька розв’язків. Sage повертає усі знайдені розв’язки у вигляді списку.
sage: solve( x^2 + x == 6, x)
[x == -3, x == 2]
sage: solve(2*x^2 - x + 1 == 0, x)
[x == -1/4*I*sqrt(7) + 1/4, x == 1/4*I*sqrt(7) + 1/4]
sage: solve( exp(x) == -1, x)
[x == I*pi]
Набір розв’язків системи нерівностей складається із об’єднання та перетинів відкритих інтервалів.
sage: solve( x^2 - 6 >= 3, x )
[[x <= -3], [x >= 3]]
sage: solve( x^2 - 6 <= 3, x )
[[x >= -3, x <= 3]]
Команда solve() намагатиметься за можливості представити розв’язок рівняння без використання чисел із плаваючою комою. Якщо це неможливо, розв’язок виражається у символьній формі.
sage: solve( sin(x) == x, x)
[x == sin(x)]
sage: solve( exp(x) - x == 0 , x)
[x == e^x]
sage: solve( cos(x) - sin(x) == 0 , x)
[sin(x) == cos(x)]
sage: solve( cos(x) - exp(x) == 0 , x)
[cos(x) == e^x]
Для знаходження чисельного наближення до розв’язку можна використати команду find_root(). Її застосування вимагає задання як виразу, так і замкненого інтервалу для пошуку розв’язку.
sage: find_root(sin(x) == x, -pi/2 , pi/2)
0.0
sage: find_root(sin(x) == cos(x), pi, 3*pi/2)
3.9269908169872414
Ця команда повертає тільки один розв’язок на вказаному інтервалі, якщо він існує. Вона не відшукає повного набору розв’язків на множині усіх дійсних чисел. Для знаходження усіх розв’язків треба використати команду find_root() послідовно для кількох інтервалів, які ще треба розумно вибрати. Нажаль, Sage не буде думати за нас. Принаймні до версії Sage 10 ця можливість ппоки що не передбачається.
Декларування змінних¶
У попередньому розділі було розглянуто рівняння з однією змінною, за яку ми завжди обирали 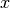 . На початку сесії Sage створює одну символьну змінну,
. На початку сесії Sage створює одну символьну змінну, 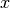 , яку можна використати для розв’язання рівнянь. Але якщо потрібні додаткові символьні змінні, їх необхідно декларувати за допомогою команди
, яку можна використати для розв’язання рівнянь. Але якщо потрібні додаткові символьні змінні, їх необхідно декларувати за допомогою команди var(). У якості імені змінної може стояти літера або набір літер і цифр.
sage: y,z,t = var("y z t")
sage: phi, theta, rho = var("phi theta rho")
sage: x1, x2 = var("x1 x2")
Примітка
Імена змінних не можуть містити пробіли. Так, рядок “square root” є недопустимим іменем змінної, але ім’я “square_root” - дозволяється.
Спроба використати символьну змінну до її декларування приводить до помилки NameError.
sage: u
...
NameError: name 'u' is not defined
sage: solve (u^2-1,u)
NameError Traceback (most recent call last)
NameError: name 'u' is not defined
Можна відмінити декларування символьної змінної, наприклад, змінної phi у прикладі вище за допомогою команди restore().
sage: restore('phi')
sage: phi
...
NameError: name 'phi' is not defined
Рівняння з кількома невідомими¶
Невеликі системи лінійних рівнянь теж можна розв’язати за допомогою solve(), якщо задекларовані усі символьні змінні. Систему рівнянь треба задати у вигляді списку, за яким йде перелік символьних змінних. Результат може містити один єдиний розв’язок, нескінченну кількість розв’язків, або не мати розв’язків взагалі.
sage: solve( [3*x - y == 2, -2*x -y == 1 ], x,y)
[[x == (1/5), y == (-7/5)]]
sage: solve( [ 2*x + y == -1 , -4*x - 2*y == 2],x,y)
[[x == -1/2*r1 - 1/2, y == r1]]
sage: solve( [ 2*x - y == -1 , 2*x - y == 2],x,y)
[]
У другому рівнянні вище r1 позначає довільну змінну, що параметризує набір розв’язків. Якщо у розв’язок входить кілька довільних змінних, то у Sage вони нумеруються послідовно як r1,r2,..., rk.
sage: solve([ 2*x + 3*y + 5*z == 1, 4*x + 6*y + 10*z == 2, 6*x + 9*y + 15*z == 3], x,y,z)
[[x == -5/2*r1 - 3/2*r2 + 1/2, y == r2, z == r1]]
Для великих систем рівнянь функція solve() може працювати вкрай повільно. Для таких систем більш доцільно використовувати функції лінійної алгебри, які у даному випадку дають кращі результати.
Вирішення нерівностей із кількома змінними може привести до дуже складних виразів, оскільки такі нерівності можуть визначати складні за формою багатовимірні інтервали. У подальшому прикладі розв’язок, який дає Sage, є списком, який містить точки перетину прямих, два промені і область, обмежену двома променями.
sage: solve([ x-y >=2, x+y <=3], x,y)
[[x == (5/2), y == (1/2)], [x == -y + 3, y < (1/2)], [x == y + 2, y < (1/2)], [y + 2 < x, x < -y + 3, y < (1/2)]]
sage: solve([ 2*x-y< 4, x+y>5, x-y<6], x,y)
[[-y + 5 < x, x < 1/2*y + 2, 2 < y]]
Вправи:
Знайдіть усі розв’язки рівняння
.
Знайдіть повний набір розв’язків нерівності
.
Знайдіть усі
та
, що задовільняють умовам
та x - 3y = -16.
За допомогою
find_root()знайдіть розв’язок рівнянняна інтервалі
.
Змініть команду так, щоби
find_root()знайшла інші розв’язки у цьому самому інтервалі.
Математичний аналіз¶
Необхідно знати розділи Основні арифметичні дії, Стандартні функції і сталі і Декларування змінних
У наборі Sage є багато команд із області диференціального і інтегрального числення. Ми розглянемо ці команди і спочатку задамо кілька функцій, що далі будуть використані у цій главі.
sage: f(x) = x*exp(x)
sage: f
x |--> x*e^x
sage: g(x) = (x^2)*cos(2*x)
sage: g
x |--> x^2*cos(2*x)
sage: h(x) = (x^2 + x - 2)/(x-4)
sage: h
x |--> (x^2 + x - 2)/(x-4)
У Sage запис x |--> вказує на то, що результуючий вираз є функцією, а не, скажімо, числом або рядком. Це означає, що такі вирази можна обчислювати так само, як і будь-яку функцію.
sage: f(1)
e
sage: g(2*pi)
4*pi^2
sage: h(-1)
2/5
Після задання цих функцій розглянемо обчислення їхніх границь у Sage.
Границі¶
Границя 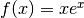 при
при 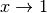 у Sage обчислюється шляхом введення такої команди:
у Sage обчислюється шляхом введення такої команди:
sage: limit(f, x=1)
e
Те саме можна зробити і з 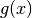 . Для обчислення ліміту виразу
. Для обчислення ліміту виразу 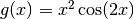 при
при 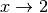 вводимо:
вводимо:
sage: limit(g, x=2)
4*cos(4)
Але функції 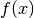 і
і 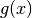 не є аж такими цікавими із точки зору обчислення границь, оскільки вони обидві неперервні для усіх дійсних чисел. Але функція
не є аж такими цікавими із точки зору обчислення границь, оскільки вони обидві неперервні для усіх дійсних чисел. Але функція 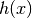 є розривною у
є розривною у 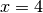 , і для дослідження її поведінки в околі точки розриву ми розглянемо границю
, і для дослідження її поведінки в околі точки розриву ми розглянемо границю 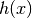 при
при 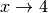 :
:
sage: limit(h, x = 4)
Infinity
Цей приклад показує, що у системах алгебраїчних обчислень слід бути подекуди уважним. Показане граниче значення є не зовсім коректним - див. нижче графік 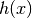 біля точки розриву.
біля точки розриву.

Точка 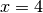 є вертикальною асимптотою, тобто функція в її околі прямує до плюс нескінченності при
є вертикальною асимптотою, тобто функція в її околі прямує до плюс нескінченності при 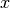 більшому від
більшому від 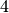 , і до мінус нескінченності при
, і до мінус нескінченності при 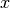 , меншому від
, меншому від 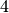 . Ми можемо обчислити*односторонні* границі, вказуючи додатковий аргумент dir.
. Ми можемо обчислити*односторонні* границі, вказуючи додатковий аргумент dir.
sage: limit(h, x=4, dir="right")
+Infinity
sage: limit(h, x=4, dir="left")
-Infinity
Похідні¶
Далі ми будемо обчислювати похідні від заданих раніше функцій. Наприклад, для отримання 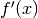 ,
, 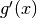 , і
, і 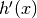 використовується одна і та сама команда
використовується одна і та сама команда derivative().
sage: fp = derivative(f,x)
sage: fp
x |--> x*e^x + e^x
sage: gp = derivative(g, x)
sage: gp
x |--> -2*x^2*sin(2*x) + 2*x*cos(2*x)
sage: hp = derivative(h,x)
sage: hp
x |--> (2*x + 1)/(x - 4) - (x^2 + x - 2)/(x - 4)^2
Перший її аргумент - це функція, яку треба продиференціювати, а другий - змінна, по якій береться похідна. Наприклад, якщо задати якусь іншу змінну, відмінну від x, Sage буде вважати 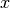 константою і продиференціює по заданій змінній.
константою і продиференціює по заданій змінній.
sage: y = var('y')
sage: derivative(f,y)
x |--> 0
sage: derivative(g,y)
x |--> 0
sage: derivative(h,y)
x |--> 0
Команда derivative() повертає іншу функцію, над якою можна робити стандартні обчислювальні операції, як і над будь-якою іншою.
sage: fp(10)
11*e^10
sage: gp(pi/2)
-pi
sage:
sage: hp(10)
1/2
Післе обчислення похідної функції можна знайти критичні точки за допомогою команди solve().
sage: solve( fp(x) == 0, x)
[x == -1, e^x == 0]
sage: solve( hp(x) == 0, x)
[x == -3*sqrt(2) + 4, x == 3*sqrt(2) + 4]
sage: solve( gp(x) == 0, x)
[x == 0, x == cos(2*x)/sin(2*x)]
Важливою прикладною задачею є побудова дотичної до функції в деякій точці 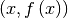 . Sage це робить легко. Наприклад, наступна команда будує пряму, дотичну до
. Sage це робить легко. Наприклад, наступна команда будує пряму, дотичну до 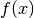 у точці
у точці 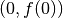 .
.
sage: T_f = fp(0)*( x - 0 ) + f(0)
sage: T_f
x
Те ж саме можна зробити для 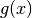 та
та 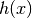 .
.
sage: T_g = gp(0)*( x - 0 ) + g(0)
sage: T_g
0
sage: T_h = hp(0)*( x - 0 ) + h(0)
sage: T_h
-1/8*x + 1/2
Інтеграли¶
Sage може обчислювати як визначені, так і невизначені інтеграли від багатьох відомих функцій. Ми почнемо з невизначенних інтегралів, які ще мають назву первісних, від кожної з заданих раніше функцій. Первісну можна обчислити за допомогою команди integral() із аргументами, аналогічними аргументам команди derivative().
sage: integral(f,x)
x |--> (x - 1)*e^x
sage: integral(g, x)
x |--> 1/4*(2*x^2 - 1)*sin(2*x) + 1/2*x*cos(2*x)
sage: integral(h, x)
x |--> 1/2*x^2 + 5*x + 18*log(x - 4)
У якості результату повертається тільки одна з первісних даннної функції. Всі інші первісні відрізняються від неї на константу. Можна перевірити, що результат дійсно є первісною, якщо знайти похідну від отриманих невизначених інтегралів.
sage: derivative(integral(f,x), x )
x |--> (x - 1)*e^x + e^x
sage: f
x |--> x*e^x
sage: derivative(integral(g,x), x )
x |--> 1/2*(2*x^2 - 1)*cos(2*x) + 1/2*cos(2*x)
sage: derivative(integral(h,x), x )
x |--> x + 18/(x - 4) + 5
Втім на перший погляд жоден з цих результатів не виглядає правильно. Але після простих алгебраїчних перетворень, а також використання тригонометричних рівностей у випадку виразу 1/2*(2*x^2 - 1)*cos(2*x) + 1/2*cos(2*x) можна переконатись, що результати тотожні із вихідними виразами.
Слід також пам’ятати, що є певний клас неперервних функцій, для яких інтеграл не існує у замкненій формі. Типовий приклад - це функція 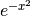 , що є базисом нормального розподілу, який широко застосовується у статистиці. Первісна від
, що є базисом нормального розподілу, який широко застосовується у статистиці. Первісна від 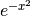 має спеціальне позначення
має спеціальне позначення 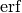 і носить також назву функції помилок.
і носить також назву функції помилок.
sage: y(x) = exp(-x^2)
sage: integral(y,x)
x |--> 1/2*sqrt(pi)*erf(x)
Також можна обчислити визначені інтеграли від заданих раніше функцій. Для цього необхідно вказати границі інтегрування як додаткові аргументи.
sage: integral(f, x,0,1)
x |--> 1
sage: integral(g,x,0,1)
x |--> 1/4*sin(2) + 1/2*cos(2)
sage: integral(h, x,0,1)
x |--> 18*log(3) - 18*log(4) + 11/2
У кожному з наведених вище прикладів Sage у якості результата повертає функцію. Кожна з цих функцій є стала функція, як і слід було чекати. Як було вказано раніше, Sage повертає вираз, що зберігає максимальну можливу точність і у якому не використовуються десяткові числа, якщо це не вказано явно. Можна швидко позначити, що потрібен саме наближений вираз, якщо помістити команду integrate() у “обгортку” з команди для наближених обчислень n().
sage: n(integral(f, x,0,1))
1.00000000000000
sage: n(integral(g, x,0,1))
0.0192509384328492
sage: n(integral(h, x,0,1))
0.321722695867944
Вправи:
Обчисліть за допомогою Sage наступні ліміти:
За допомогою Sage обчисліть наступні похідні відносно вказанних змінних:
(пам’ятайте, що слід декларувати змінну ``t``)
За допомогою Sage обчисліть наступні інтеграли
Статистика¶
Необхідно знати розділ Основні арифметичні дії
У цьому розділі розглянемо деякі основні функції дескриптивної статистики, наявні у Sage.
Для прикладів із використанням цих функцій спочатку згенеруємо послідовність псевдовипадкових цілих чисел від 0 до 100. Функція random() повертає випадкове число у інтервалі 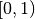 , але ми використаємо математичний прийом для отримання за допомогою цієї функції саме цілих чисел у потрібному нам інтервалі. Нагадаємо, що алгоритм генерації випадкових чисел при виконанні вправи буде давати список, відмінний від показаного у прикладі.
, але ми використаємо математичний прийом для отримання за допомогою цієї функції саме цілих чисел у потрібному нам інтервалі. Нагадаємо, що алгоритм генерації випадкових чисел при виконанні вправи буде давати список, відмінний від показаного у прикладі.
sage: data = [ int(random()*(100-0) + 0) for i in [ 1 .. 20 ] ]
sage: data
[78, 43, 6, 50, 47, 94, 37, 70, 66, 32, 1, 34, 93,
30, 99, 82, 22, 74, 18, 40]
Тепер можна обчислити середнє, медіану, моду, варіацію і стандартне відхилення отриманних даних.
sage: mean(data)
254/5
sage: median(data)
45
sage: mode(data)
[32, 1, 66, 99, 82, 37, 6, 40, 74, 43,
34, 78, 47, 50, 30, 22, 18, 70, 93, 94]
sage: variance(data)
83326/95
sage: std(data)
sqrt(83326/95)
Зауважимо, що стандартне відхилення і варіація обчислюються у формі незміщеної оцінки. Якщо необхідно включити зміщення, можна додати до команди опцію bias=True.
Також за допомогою команди moving_average() можна обчислити рухоме (‘ковзаюче’) середнє для набору даних.
sage: moving_average(data,4)
[177/4,73/2,197/4,57,62,267/4,205/4,169/4,
133/4,40,79/2,64,76,233/4,277/4,49,77/2]
sage: moving_average(data,10)
[523/10, 223/5,437/10,262/5,252/5, 278/5,
272/5,529/10,533/10,97/2,493/10]
sage: moving_average(data,20)
[254/5]
Вправи:
Згенеруйте за допомогою Sage список з 20 випадкових цілих чисел.
Значення зросту восьми студентів (в дюймах) складають
. Знайдіть середнє, медіану та моду для цього розподілу даних.
Для тих самих даних обчисліть стандартне відхилення та варіацію значень зросту.
Знайдіть діапазон значень зросту (використайте команди
max()таmin())
Побудова графіків¶
2D-графіка¶
Необхідно знати розділи Стандартні функції і сталі та Розв’язування рівнянь і нерівностей
У Sage передбачено багато способів візуалізації результатів математичних обрахунків. У цьому розділі ми швидко пройдемо деякі основні команди для побудови графіків функцій та роботи із зображеннями.
Щоб побудувати мінімалістичний графік функції 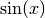 на проміжку від
на проміжку від 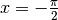 до
до 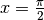 , використовується команда
, використовується команда plot().
sage: f(x) = sin(x)
sage: p = plot(f(x), (x, -pi/2, pi/2))
sage: p.show()

Якщо не вказано інше, отриманий графік буде без жодних прикрас. Проте до нього можно додати мітки осей та змінити колір лінії графіка, наприклад, на рожевий, редагуючи атрібути графіка із додаванням опцій axes_labels та color.
sage: p = plot(f(x), (x,-pi/2, pi/2), axes_labels=['x','sin(x)'], color='purple')
sage: p.show()

Опція color приймає аргументи у вигляді рядка-позначення кольору (‘purple’, ‘green’, ‘red’, ‘black’ та ін.), трійку чисел RGB (.25,.10,1), або 16-річне позначення кольору типу #ff00aa, як у HTML.
За допомогою опцій linestyle та thickness можна явно задати стиль креслення лінії - суцільна або пунктирна, а також її товщину.
sage: p = plot(f(x), (x,-pi/2, pi/2), linestyle='--', thickness=3)
sage: p.show()

Додаючи графіки двох функцій, ми можемо відобразити їх разом на тій самій координатній сітці.
sage: f(x) = sin(x)
sage: g(x) = cos(x)
sage: p = plot(f(x),(x,-pi/2,pi/2), color='black')
sage: q = plot(g(x), (x,-pi/2, pi/2), color='red')
sage: r = p + q
sage: r.show()
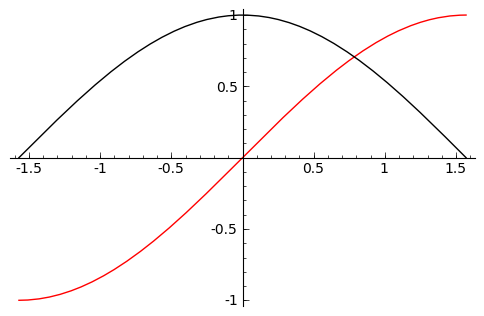
Для поєднання команд побудови графіків із матеріалом, викладеним раніше, використаймо команду find_root() і знайдемо точку перетину функцій 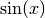 та
та 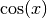 . Потім ми додамо цю точку до графіку та поставимо при ній мітку.
. Потім ми додамо цю точку до графіку та поставимо при ній мітку.
sage: find_root( sin(x) == cos(x),-pi/2, pi/2 )
0.78539816339744839
sage: P = point( [(0.78539816339744839, sin(0.78539816339744839))] )
sage: T = text("(0.79,0.71)", (0.78539816339744839, sin(0.78539816339744839) + .10))
sage: s = P + r + T
sage: s.show()

При побудові графіка Sage за замовчуванням реалізує низку його деталей, які багато у чому відповідають нашим інтуїтивним очікуванням “середнього” графіка. Але природно, що у багатьох випадках автоматично побудований малюнок не буде у повній мірі задовільняти нашим вимогам.
sage: f(x) = (x^3 + x^2 + x)/(x^2 - x -2 )
sage: p = plot(f(x), (x, -5,5))
sage: p.show()
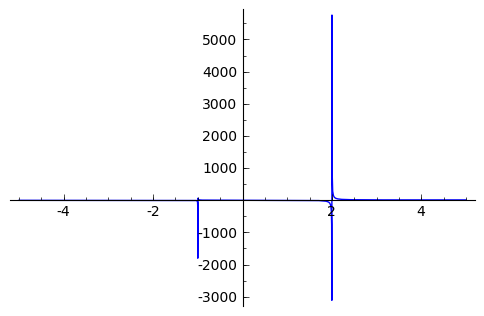
Завдяки асимптотичній поведінці цієї функції Sage змінює масштаб по осях графіка, щоб мати змогу зобразити великі значення 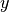 в околі
в околі 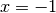 та
та 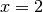 . Це приховує багато деталей поведінки графіка функції. Щоб запобігти цьому, можна вказати у явному вигляді границі діапазонів зміни функції по вертикалі і по горизонталі
. Це приховує багато деталей поведінки графіка функції. Щоб запобігти цьому, можна вказати у явному вигляді границі діапазонів зміни функції по вертикалі і по горизонталі
sage: p.show(xmin=-2, xmax=4, ymin=-20, ymax=20)

Нам здається, що так особливості цієї функції виявляються краще.
У Sage за допомогою команди parametric_plot() можна будувати параметричні графіки. Нижче у такий спосіб побудовано звичайне коло із радіусом 3.
sage: t = var('t')
sage: p = parametric_plot( [3*cos(t), 3*sin(t)], (t, 0, 2*pi) )
sage: p.show()
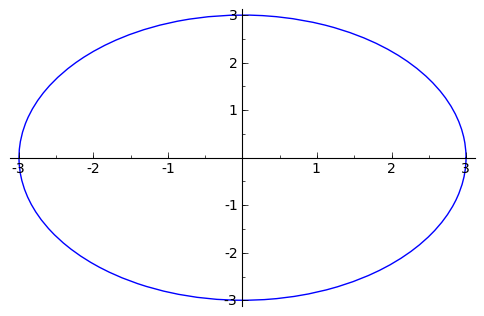
Встановлене по замовчуванню співвідношення масштабів осей очевидно спотворює форму цієї фігури. Цьому можна зарадити, явно задаючи опцію aspect_ratio.
sage: p.show(aspect_ratio=1)
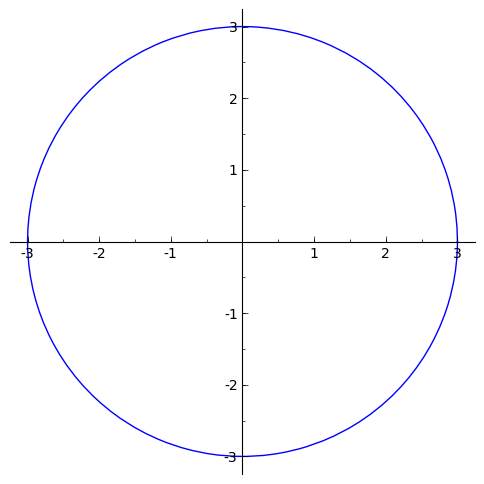
Інші наявні команди для побудови графіків можуть приймати багато тих самих опцій, що і команда plot. У наступному прикладі викреслюється крива Ліссажу 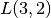 із заданням параметрів лінії як товстої червоної пунктирної.
із заданням параметрів лінії як товстої червоної пунктирної.
sage: p = parametric_plot( [sin(3*t), sin(2*t)], (t, 0, 3*pi), thickness=2, color='red', linestyle="--")
sage: p.show()
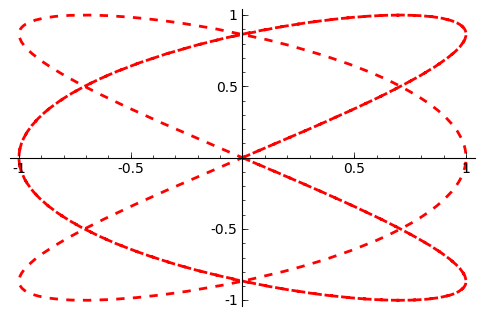
Полярні графіки викреслюються за допомогою команди polar_plot().
sage: theta = var("theta")
sage: r(theta) = sin(4*theta)
sage: p = polar_plot((r(theta)), (theta, 0, 2*pi) )
sage: p.show()

І накінець, Sage вміє креслити неявно задані функції. Наприклад, для зображення геометричного місця точок 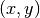 , що задовільняють рівняння
, що задовільняють рівняння 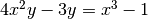 , можна ввести наступну команду:
, можна ввести наступну команду:
sage: implicit_plot(4*x^2*y - 3*y == x^3 - 1, (x,-10,10),(y,-10,10))
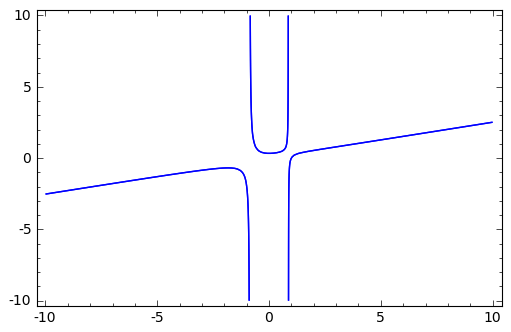
Вправи:
Накресліть графік функції
для
товстою червоною лінією.
Накресліть графік функції
у тому самому інтервалі товстою синьою лінією.
Зобразіть ці два графіки разом на одній і тій самій координатній сітці.
Накресліть графік функції
для
і підберіть діапазони значень так, щоб графік займав тільки інтервал
.
За допомогою команд із цього розділу побудуймо наступний малюнок:

3D графіка¶
3D-графіки можна побудувати за допомогою команди plot3d()
sage: x,y = var("x y")
sage: f(x,y) = x^2 - y^2
sage: p = plot3d(f(x,y), (x,-10,10), (y,-10,10))
sage: p.show()
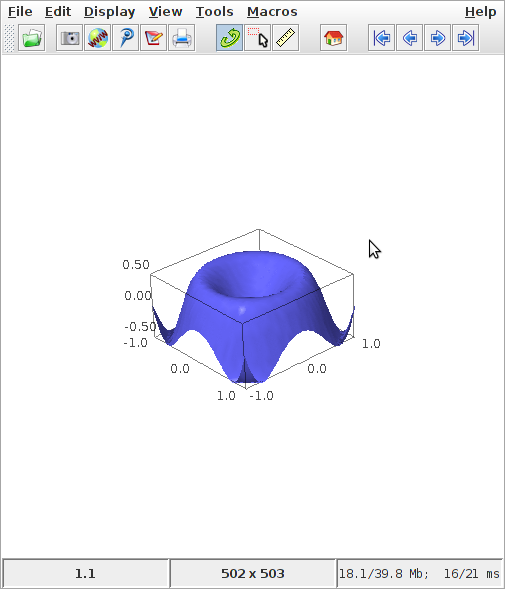
Sage працює із тривимірною графікою дещо по-іншому, ніж ми бачили раніше. За допомогою програми jmol можна згенерувати інтерактивні графіки. Таким чином замість статичної картинки ми бачимо або вікно, подібне до показаного вище, або, якщо Sage використовується з інтерфейсом блокноту, то відповідний Java-аплет у вікні браузера.
У Sage є корисна функція інтерактивного повороту графіка, що відбувається шляхом кліку на поверхню функції і перетягування її у напрямку повороту. Зменшення або збільшення масштабу зображення відбувається поворотом коліщатка миші (або проведенням по сенсорній панелі двома пальцями у вертикальному напрямку на комп’ютерах Mac). Після повороту і вибору масштабування графіка його можна зберегти до файлу. Для цього потрібно зробити клік правою кнопкою миші у будь-якому місці вікна або аплету і вибрати опцію збереження (save) як малюнок PNG, як показано нижче.

Примітка
Якщо Sage запускається під Windows або на sagenb.org, тоді файл зберігається відповідно на віртуальній машині VMware або на sagenb.org.
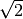
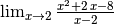

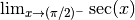
![\frac{d}{dx}\left[ x^{2}e^{3x}\cos(2x) \right]](_images/math/e203c23070c48bdd98b7734a8c00247428907d61.png)
![\frac{d}{dy}\left[ x\cos(x)\right]](_images/math/4ef14ae3d98c17ed1326d40414d16cf2f5cabf54.png)