Знайомство з підручником

Вступ

Як користуватися цим підручником

Підручник розділено на чотири частини. У поточній частині, Знайомство з підручником, наводяться деякі основні відомості про Sage, проводиться ознайомлення читача із структурою самого підручника та пропонуються можливі варіанти участі у проекті.

Друга частина, Sage як калькулятор, охоплює такі теми, як арифметичні дії, обчислення функцій, побудова простих графіків, розв’язання рівнянь та інші теми математичного аналізу початкового рівня. Цей розділ названо Sage як калькулятор, тому що більшість прикладів з нього зазвичай розв’язуються за допомогою калькулятора із функцією побудови графіків. Цей розділ буде корисний, перш за все, тим, хто ще не дістався математичного аналізу, або щойно почав його вивчати.

Програмування у Sage знайомить читача із більш складними темами. Наприклад, як Sage працює із числами, як задавати та використовувати змінні та функції, як працювати зі списками, рядками та множинами, а також що таке всесвіти та перетворення типів у Sage.

Остання частина, Математичні структури, висвітлює теми, що їх зазвичай викладають у вищих навчальних закладах: лінійна алгебра, теорія чисел, груп, кілець, полів і т.ін.

Оскільки це підручник, він містить багато прикладів для ілюстрації матеріалу, тому автори радять читачеві паралельно із читанням виконувати розглянуті команди у Sage на комп’ютері. Окрім прикладів для пояснення, автори намагалися підібрати задачі для самостійного розв’язання, що допоможуть краще розібратися у темі. Також ми рекомендуємо читачеві якомога більше практикуватись в них.

Хоча матеріал у цьому підручнику здебільшого викладено від простого до складного, на початку кожного розділу автори надають список найважливіших тем, на які він спирається. Посилання, що містяться у списку після напису “Ви вже маєте знати.”, ведуть до відповідних розділів підручника. Окрім цього, автори намагалися зібрати корисні посилання на інші матеріали в Інтернеті. Такі посилання містяться після слів “Див. також:”.

Подекуди в тексті зустрічаються нумеровані посилання (наприклад, “[1]”). Список таких посилань завжди наводиться після відповідного розділу та вказує на додаткові матеріали, що містять більш детальний розгляд позначених питань.

Посилання:

[1]	William A. Stein et al. Sage Mathematics Software (Version 4.7.1), The Sage Development Team, 2011, http://www.sagemath.org.

Перші кроки

Про Sage

Sage – це система комп’ютерної математики із відкритим кодом, побудована на мові програмування Python. Її було започатковано для дослідницької роботи в області математики, але згодом вона переросла у потужний інструмент і для навчання. Вона об’єднує у собі багато окремих математичних пакетів, надаючи єдиний інтерфейс до них за допомогою мови Python . Тож вивчаючи Sage, ви заразом вивчаєте і Python.

Як і багато інших відкритих проектів, Sage пропонує усім своїм користувачам взяти участь у розробці. Цей підручник є одним із багатьох джерел інформації про використання Sage. Більш детальну інформацію див. на веб-сторінці Sage.

Впродовж усього підручника вважається, що читач має доступ до робочого середовища Sage. Встановлення Sage у більшості випадків зводиться до завантаження відповідного архіву із офіційної веб-сторінки, розпакування його та запуску команди sage. Подробиці процесу встановлення на різні системи див. на сторінці Installation Guide.

У сеансі Sage є два шляхи виконання команд: безпосередньо з командного рядка або за допомогою веб-інтерфейсу Notebook. Notebook (блокнот) візуально схожий на інтерфейси Matlab, Mathematica та Maple і є популярним вибором користувачів.

Все, що йде у тексті за запрошенням командного рядка (sage:), є командою, яку можна набрати у середовищі Sage. Наприклад, якщо потрібно розкласти ціле число на множники (факторизувати), можна скористатися командою factor()

sage: factor(1438880)
2^5 * 5 * 17 * 23^2

У рядку після sage: міститься результат виконання відповідної команди.

При роботі із командним рядком вивід терміналу виглядає приблизно так:

Натомість взаємодія із графічним середовищем блокноту має приблизно такий вигляд:

Автодоповнення рядка

Далі розглянемо, як використовувати деякі основні можливості обох інтерфейсів: доповнення рядка та вбудовану систему довідки.

Однією із зручних функцій Sage є автодоповнення команд. Скористатися ним можна, якщо ввести перші літери бажаної команди та натиснути після цього клавішу TAB. Нехай потрібно обрахувати 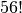, але ми не пам’ятаємо, якою командою це можна зробити. Але логічно було би припустити, що потрібна команда міститиме слово factorial. Для перевірки цього припущення достатньо ввести fac та натиснути клавішу TAB.

sage: fac[TAB]
factor     factorial
sage: factor

Результат показує, що на літери fac починаються лише дві команди Sage: factor() та factorial(). Зверніть увагу, що Sage вже продовжив команду від початкового fac до factor, адже це спільний початок обох наявних команд. Оскільки factorial більш схоже на шуканий варіант, оберемо його, ввівши наступну літеру i та натиснувши клавішу TAB знову.

sage: factorial

Цього разу ми вже не отримали ніякого списку, тому що єдиною командою, що починається на factori є factorial(). Отже для обрахунку 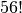потрібно просто доповнити команду аргументом (56).

sage: factorial(56)
710998587804863451854045647463724949736497978881168458687447040000000000000

Ще одне корисне застосування клавіші табуляції – це виявлення методів певного об’єкту. Нехай у нас задане ціле число 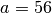і ми хочемо дізнатись, які команди є в Sage для роботи із цілими, такими, як . У цьому випадку об’єктом є . Щоб вивести усі методи, асоційовані з цілим типом, можна ввести a., після чого натиснути клавішу табуляції.

sage: a = 56
sage: a.[TAB]
a.N                            a.kronecker
... A long list of Commands ...
a.divisors                     a.parent
a.dump                         a.popcount
a.dumps                        a.powermod
a.exact_log                    a.powermodm_ui
--More--

При цьому виводиться досить довгий список команд: Sage – дуже потужна система, і вміє багато чого робити із цілими числами. Слово --More-- у нижній частині екрану позначає, що список можливих команд є задовгий для одного екрану. Для посторінкової прокрутки цього списку натисніть будь-яку клавішу, і Sage перейде до наступної сторінки.

На другій сторінці ми бачимо метод factor(). Для того, щоб застосувати цей метод, який факторизує (розкладає на прості множники) , ми вводимо a.factor().

sage: a.factor()
2^3 * 7

Тож автодоповнення не тільки зменшує обсяг ручного набору, але і допомагає знаходити нові невідомі вам команди в Sage.

Довідка за допомогою ?

Після знаходження потрібної команди наступним кроком буде з’ясування, що саме робить команда та як правильно її використовувати. Sage має вбудовану систему довідки, яка допоможе у цьому.

Припустимо, нам треба обчислити найменше спільне кратне двох цілих чисел, але ми не впевнені щодо команди для цього. Пошук можна почати, натиснувши у командному рядку l, і після цього – клавішу табуляції.

sage: l[TAB]
laguerre                    list_plot3d
lambda                      lk
laplace                     ll
latex                       ln
lattice_polytope            lngamma
lazy_attribute              load
lazy_import                 load_attach_path
lc                          load_session
lcalc                       loads
lcm                         local/LIB
ldir                        local/bin
...
lisp_console                ls
list                        lucas_number1
list_composition            lucas_number2
list_plot                   lx

Знову перед нами з’явився достатньо довгий список команд, з якого потрібно щось вибрати. Прокручуємо список донизу – і бачимо далі команду lcm(), яка, як ми припускаємо, може зробити те, що нам потрібно. Введемо тоді lcm?.

sage: lcm?

При виконанні цієї команди виводиться сторінка із поясненнями щодо використання та призначення команди.

Base Class:     <type 'function'>
String Form:    <function lcm at 0x32db6e0>
Namespace:      Interactive
File:           /home/ayeq/sage/local/lib/python2.6/site-packages/sage/rings/arith.py
Definition:     lcm(a, b=None)
Docstring:
       The least common multiple of a and b, or if a is a list and b is
       omitted the least common multiple of all elements of a.

       Note that LCM is an alias for lcm.

       INPUT:

       * ``a,b`` - two elements of a ring with lcm or

       * ``a`` - a list or tuple of elements of a ring with lcm

       EXAMPLES:

          sage: lcm(97,100)
          9700
          sage: LCM(97,100)

Ми знову отримаємо багато інформації - зазвичай більше, ніж вміщується на одному екрані. Навігація з командного рядка дуже проста: за допомогою клавіші “Пробіл” можна перейти до наступної сторінки, b, або “Стрілка вгору” - це перехід назад. Для виходу із довідки треба натиснути клавішу q.

При перших кроках варто переглянути розділи: опис, INPUT та EXAMPLES. В описі наводиться короткий перегляд того, що робить ця команда. Розділ INPUT дає відомості про аргументи команди, а в розділі EXAMPLES можна знайти приклади її використання.

У цьому випадку опис виглядає так:

The least common multiple of a and b, or if a is a list and b is
omitted the least common multiple of all elements of a.
Note that LCM is an alias for lcm.

З цього опису вже цілком зрозуміло, що йдеться саме про шукану команду. Тепер зазирнемо до розділу INPUT:

INPUT:
* ``a,b`` - two elements of a ring with lcm or
* ``a`` - a list or tuple of elements of a ring with lcm

Тут ми бачимо, що команда lcm приймає або два аргументи, у нашому випадку - два цілі числа, або список об’єктів. І, в кінці кінців, розділ EXAMPLES дає уявлення про те, як цю команду використовують на практиці.

EXAMPLES:

   sage: lcm(97,100)
   9700
   sage: LCM(97,100)
   9700
   sage: LCM(0,2)
   0
   sage: LCM(-3,-5)
   15
   sage: LCM([1,2,3,4,5])
   60
   sage: v = LCM(range(1,10000))   # *very* fast!
   sage: len(str(v))
   4349

Така пропрацьована і докладна система вбудованої довідки є однією з найбільших переваг Sage; що швидше ми до неї звикнемо, то легше ми зможемо перейти до повноцінного використання цієї системи комп’ютерних обчислень.

Вихідний код функції, ??

Дивись також

Скрінкасти Sage

Внесок у розвиток цього підручника

Ми вітаємо зусилля з покращення цього підручника, а також пропозиції про додаткові теми, які варто у нього включити.

Код джерела цієї веб-сторінки можна знайти на сторінці веб-хостингу проекту bitbucket. Тут знаходиться повна копія коду джерела, необхідного для генерації цієї веб-сторінки. Для побудови сторінки із джерела потрібно встановити програмний пакет Sphinx Documentation, написаний на мові програмування Python. Ми були б раді побачити будь-які ваші зміни та доповнення до підручника і просимо повідомити за цією адресою про нові матеріали, що ви додали. Ми намагаємося зробити цей підручник всеохоплюючим наскільки це можливо, і тому вітаємо будь-яку поміч зі сторони.

Цей підручник написано із використанням мови розмітки reStructuredText, текстові файли якої обробляються за допомогою програмного пакету Sphinx із отриманням кінцевого продукту у вигляді файлів HTML або PDF. Як Sphinx, так і reStructuredText скрізь використовуються і в офіційній документації Sage і Python, тому деякі основні відомості про них варто мати усім, хто тим чи іншим способом приймає участь у розвитку цих проектів.

Підручник складається із чотирьох частин: у розділі Знайомство з підручником містяться головні відомості про використання підручника та можливі доповнення до нього, усі інші розділи є вже суто математичними. Як видно з назви, розділ Sage як калькулятор містить вказівки щодо безпосередніх обчислень, побудови графіків, а також матеріал, що може викладатися у курсах алгебри, вступу до математичної статистики та математичного аналізу університетів. Рівень складності, на нашу думку, відповідає абітурієнту або школяру-відміннику.

“Програмування в Sage” полегшує перехід до вищих розділів математики, розглядаючи зв’язок між математичними поняттями та обчислювальною практикою. У першому розділі розглядаються “всесвіти” та перетворення типів (раціональні, реальні, булеві константи тощо); змінні; основні структури - множини, списки та рядки. У другому розділі наводяться базові поняття програмування: умовні оператори, ітеративні обчислення, прийоми роботи з файлами та даними тощо. У третьому розділі обговорюються програмні математичні пакети у Sage. І накінець коротко розглядаються можливості створення інтерактивних презентацій у середовищі блокноту.

Розділ “Математичні структури” написано на більш високому математичному рівні у порівнянні із попередніми частинами, оскільки він призначений перш за все для студентів університету, що проходять вищі розділи математичних дисциплін. Тут пропонується знайомство із певними математичними конструкціями, для яких існує відповідний клас Sage. Цей розділ можна розглядати як незалежний від інших.

Дивись також

Вступ до мови розмітки reStructuredText

Подяки, ліцензія

Оригінальний текст підручника та прикладів написав Девід Монарес під керівництвом Майка О’Салівана та за підтримки Фонду Президента Університета Сан-Дієго. Підручник поширюється за ліцензією Creative Commons Attribution-ShareAlike 3.01, а отже будь-хто має право вільно поширювати та змінювати його за умови збереження посилання на авторів та Фонд. Своє ім’я можна додати до списку нижче.

Приймали участь:

• Ryan Rosenbaum.

Перекладачі:

• Володимир Смоляр