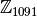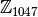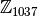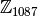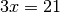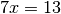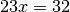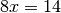Математичні структури¶
Окремі розділи цієї частини підручника відносно незалежні один від одного. Для розуміння викладеного тут матеріалу слід пройти главу Об’єкти Sage. Також корисним може бути розділ Згортання списків (цикли у списках). Крім того, у кінці, коли настане час вже робити якісь реальні дії за цим матеріалом, може придатись істотна частина глави Засоби програмування. Багато розділів у цій частині ще не завершено, тому ми будемо раді доповненням та іншій помочі від читачів.
Цілі числа і арифметичні дії із цілочисельним діленням¶
Алгебра цілих чисел за модулем 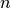 ¶
¶
Необхідно знати розділи Універсуми та приведення типів та Змінні
У цьому розділі ми розглянемо побудову 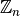 - кільця цілих чисел за модулем
- кільця цілих чисел за модулем 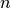 , а також деякі прості дії із такими об’єктами.
, а також деякі прості дії із такими об’єктами.
Для побудови 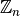 використаємо команду
використаємо команду Integers.
sage: Integers(7)
Ring of integers modulo 7
sage: Integers(100)
Ring of integers modulo 100
Обчислення за модулем деякого цілого числа завжди можна виконати, послідовно використовуючи в усіх діях оператор %, але після побудови кільця у явному вигляді усі такі операції можна представити у більш природній формі.
sage: R=Integers(13)
sage: a=R(6)
sage: b=R(5)
sage: a + b
11
sage: a*b
4
Проведенням явного перетворення типу від чисел у кільце 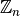 можна обчислити деякі математичні властивості елементів, наприклад, їх порядок по відношенню до операцій додавання та множення, а також чи є елемент одиницею.
можна обчислити деякі математичні властивості елементів, наприклад, їх порядок по відношенню до операцій додавання та множення, а також чи є елемент одиницею.
sage: a.additive_order()
13
sage: a.multiplicative_order()
12
sage: a.is_unit()
True
Змінна, обернена до  за операцією додавання, обчислюється за допомогою операції
за операцією додавання, обчислюється за допомогою операції -a; якщо  є одиницею, обернене до нього за операцією множення обчислюється за допомогою операції
є одиницею, обернене до нього за операцією множення обчислюється за допомогою операції a^(-1) або 1/a.
sage: (-a)
7
sage: (a^(-1))
11
Дію цих операцій можна легко перевірити. :
sage: a + (-a)
0
sage: a*(a^(-1))
1
Пригадаймо, що ділення у 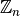 фактично є операцією множення на обернений елемент.
фактично є операцією множення на обернений елемент.
sage: R=Integers(24)
sage: R(4)/R(5)
20
sage: R(4)*R(5)^-1
20
sage: R(4/5)
20
Зрозуміло, не всі елементи мають обернені. При спробі виконати неправильне ділення Sage видає помилку
sage: R(5/4)
...
ZeroDivisionError: Inverse does not exist.
При виконанні цих дій слід бути уважним, оскільки ми задаємо Sage зробити перетворення раціонального числа у 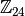 . Це може привести до неочікуваних наслідків, оскільки деякі перетворення проводяться на раціональних числах перед перетворенням типу. Наприклад, розглянемо наступну операцію:
. Це може привести до неочікуваних наслідків, оскільки деякі перетворення проводяться на раціональних числах перед перетворенням типу. Наприклад, розглянемо наступну операцію:
sage: R(20).is_unit()
False
sage: R(16/20)
20
У 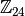 елемент
елемент 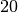 не є одиниця, хоча на перший погляд здається, що ми виконали ділення на нього. Але зверніть увагу на порядок операцій. Спочатку Sage скорочує
не є одиниця, хоча на перший погляд здається, що ми виконали ділення на нього. Але зверніть увагу на порядок операцій. Спочатку Sage скорочує 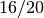 до
до 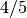 , і потім проводить перетворення типу від
, і потім проводить перетворення типу від 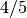 до
до 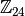 . Оскільки
. Оскільки  є одиницею у
є одиницею у 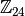 , операція виконується успішно.
, операція виконується успішно.
Можна перевірити деякі властивості кільця.
sage: R
Ring of integers modulo 24
sage: R.order()
24
sage: R.is_ring()
True
sage: R.is_integral_domain()
False
sage: R.is_field()
False
Оскільки кільце є скінченним, у Sage можна вивести усі його елементи.
sage: R = Integers(13)
sage: R.list()
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]
У цьому прикладі R - це поле, оскільки  - просте число. Якщо кільце не є полем, тоді одиниці у
- просте число. Якщо кільце не є полем, тоді одиниці у 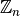 створюють групу за операцією множення. Sage може вирахувати список генераторів групи одиниць за допомогою методу
створюють групу за операцією множення. Sage може вирахувати список генераторів групи одиниць за допомогою методу unit_gens().
sage: R = Integers(12)
sage: R.uni
R.unit_gens R.unit_group_order
R.unit_group_exponent R.unit_ideal
sage: R.unit_gens()
[7, 5]
Можна також визначити порядок цієї підгрупи.
sage: R.unit_group_order()
4
На жаль, у Sage поки що немає функції, яка би повертала одиниці у 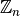 як групу. Із використанням поданої вище інформації можна у декілька способів вивести список елементів.
як групу. Із використанням поданої вище інформації можна у декілька способів вивести список елементів.
sage: (a,b) = R.unit_gens()
sage: a
7
sage: b
5
sage: [ (a^i)*(b^j) for i in range(2) for j in range(2) ]
[1, 5, 7, 11]
Також список одиниць можна отримати за допомогою згортання списку.
sage: [ x for x in R if x.is_unit()]
[1, 5, 7, 11]
Вправи
Побудуйте кільце цілих чисел за модулем
та дайте відповідь на наступні питання:
Обчисліть мультиплікативний порядок
та
.
Який з елементів зі списку вище є одиницею?
Які генератори групи одиниць?
Виведіть список усіх елементів групи одиниць.
Повторіть усі кроки обчислень знову для кільця цілих чисел за модулем
.
Напишіть функцію, що методом вичерпного пошуку визначає, чи a є одиницею за модулем n.
Для
та
визначте, які з
та
є одиницями у
. Після знаходження одиниці знайдіть її обернений елемент і порівняйте з виводом функції
. Спробуйте пояснити знайдене співвідношення.
Перевірте за допомогою Sage, чи наступні кільця є полями. У кожному прикладі опишіть одиничну групу за допомогою генераторів та відношень.
Конгруенції¶
Необхідно знати розділи Алгебра цілих чисел за модулем та Згортання списків (цикли у списках)
Лінійною конгруенцією називають рівняння виду 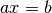 у
у 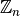 . Один із способів перевірки наявності розв’язку для задачі подібного типу - це прямий перебір. Наприклад, визначити, чи існує розв’язок
. Один із способів перевірки наявності розв’язку для задачі подібного типу - це прямий перебір. Наприклад, визначити, чи існує розв’язок 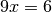 , можна таким чином:
, можна таким чином:
sage: R=Integers(21)
sage: a=R(9)
sage: 6 in [ a*x for x in R ]
True
Відмітимо, що з вищенаведеного випливає тільки існування принаймні одного розв’язку рівняння 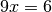 у
у 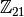 . Можна побудувати список цих розв’язків за допомогою наступного згортання списків.
. Можна побудувати список цих розв’язків за допомогою наступного згортання списків.
sage: [ x for x in R if R(9)*x == R(6)]
[3, 10, 17]
Подібним способом можна визначити, що розв’язок не існує.
sage: [ x for x in R if R(9)*x == R(2) ]
[]
Щоб отримати такі самі результати, можна також скористатись функцією solve_mod().
sage: solve_mod( 9*x == 6, 21)
[(3,), (10,), (17,)]
sage: solve_mod( 9*x == 2, 21)
[]
Функція solve_mod() працює із лінійними конгруенціями від декількох змінних.
sage: solve_mod( 9*x + 7*y == 2, 21)
[(15, 14), (15, 8), (15, 2), (15, 17), (15, 11), (15, 5), (15, 20), (1, 14), (1, 8), (1, 2), (1, 17), (1, 11), (1, 5), (1, 20), (8, 14), (8, 8), (8, 2), (8, 17), (8, 11), (8, 5), (8, 20)]
Розв’язки виводяться у формі  зі змінними у тому порядку, у якому вони зустрічаються у рівняннях.
зі змінними у тому порядку, у якому вони зустрічаються у рівняннях.
Функція solve_mod() дозволяє розв’язувати системи лінійних конгруенцій.
sage: solve_mod( [9*x + 2*y == 2, 3*x + 2*y == 11 ], 21)
[(9, 13), (16, 13), (2, 13)]
Як і у випадку команди solve(), обчислення для систем із багатьма змінними або багатьма рівняннями можуть істотно сповільнюватись. Для таких систем рекомендується застосування інструментів лінійної алгебри.
За допомогою solve_mod() можна знаходити розв’язки для нелінійних конгруенцій.
sage: solve_mod(x^2 + y^2 == 1, 7)
[(0, 1), (0, 6), (1, 0), (2, 2), (2, 5), (5, 2), (5, 5), (6, 0)]
sage: solve_mod([x^2 + y^2 == 1, x^2 - y == 2], 7)
[(2, 2), (5, 2)]
На кінець, у деяких випадках Sage може знаходити одночасний розв’язок лінійних конгруенцій із різними модулями. У цьому алгоритмі використовується китайська теорема про залишки, що реалізується командою crt(). Наприклад, наступний код обчислює найменше невід’ємне ціле число 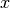 , конгруентне до
, конгруентне до 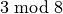 ,
, 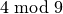 та
та 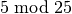 .
.
sage: crt([3,4,5],[8,9,25])
355
Командою mod() можна перевірити правильність розв’язку.
sage: mod(355,8)
3
sage: mod(355,9)
4
sage: mod(355,25)
5
Множина усіх цілочисельних розв’язків - це цілі числа, конгруентні 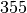 за модулем
за модулем 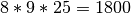 .
.
Вправи
Знайдіть усі розв’язки для наступних конгруенцій над
.
Вище було побудовано набори розв’язків для конгруенцій
,
та
. У чому їхня подібність та різниця? Чи можна на основі цих результатів зробити загальні висновки щодо структури множини
?
За допомогою команди
solve_mod()знайдіть усі розв’язки для наступних конгруенцій за модулем.
Міні-розділ: алгоритм Евкліда¶
Необхідно знати теми: Integer Division and Factoring, Змінні, External Files and Sessions та Цикли з умовою
Пригадаємо, що для 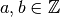 із
із 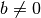 завжди існує єдина пара чисел
завжди існує єдина пара чисел  , таких, що
, таких, що 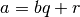 із
із 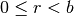 . Беручи це до уваги, за допомогою Sage обчислимо gcd (найбільший спільний дільник) двох цілих чисел за допомогою алгоритму Евкліда. Наступний код реалізує цей алгоритм у Sage.
. Беручи це до уваги, за допомогою Sage обчислимо gcd (найбільший спільний дільник) двох цілих чисел за допомогою алгоритму Евкліда. Наступний код реалізує цей алгоритм у Sage.
# Begin euclid.sage
r=a%b
print (a,b,r)
while r != 0:
a=b; b=r
r=a%b
print (a,b,r)
# End euclid.sage
Створимо файл euclid.sage із поданим вище кодом. Після завантаження цього файлу на виході з’явиться наступне:
sage: a=15; b=4
sage: load euclid.sage
(15, 4, 3) (4, 3, 1) (3, 1, 0)
sage: a=15; b=5
sage: load euclid.sage
(15, 5, 0)
У першому випадку значення gcd складає 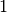 , а у другому -
, а у другому -  .
.
Вправи
Відредагуємо код у циклі у
euclid.sageтак, щоби виводилося тільки значення найбільшого спільного дільника та кількість ділень (тобто кількість кроків алгоритму). Порівняйте швидкість відпрацювання цієї версії алгоритму із вбудованою функцією Sagegcd(), порахувавши результат за допомогою цих двох функцій на парах великих цілих чисел.Напишіть власний покращений алгоритм Евкліда, відповідно змінивши код циклу у
euclid.sage.
Групи¶
У Sage реалізовано три великі типи груп: PermutationGroup() (групи перестановок), MatrixGroup() (матричні) та AbelianGroup() (абелеві групи). Ми почнемо із груп перестановок і розглянемо більшість методів, що можуть бути застосовані до них. Багато з цих методів можна застосувати до довільних груп, тому наступні розділи будуть дещо скороченими із увагою більше на методи, специфічні для саме тих структур.
Дивись також
Group Theory and Sage: A Primer - “Вступ до теорії груп та її застосування у Sage”, Rob Beezer
Симетричні групи¶
Симетричною групою 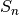 називається група перестановок на
називається група перестановок на 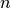 елементах. Спочатку ми створимо симетричну групу на
елементах. Спочатку ми створимо симетричну групу на 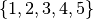 . Це робиться за допомогою команди
. Це робиться за допомогою команди SymmetricGroup.
sage: S5 = SymmetricGroup(5)
S5 Symmetric group of order 5! as a permutation group
Після побудови групи порахуємо кількість її елементів, що дорівнює 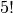 , і випишемо їх.
, і випишемо їх.
sage: S5.cardinality()
120
sage: S5.list()
[(), (4,5), (3,4), (3,4,5), (3,5,4), (3,5), (2,3), (2,3)(4,5), (2,3,4), (2,3,4,5), (2,3,5,4), (2,3,5), (2,4,3), (2,4,5,3), (2,4), (2,4,5), (2,4)(3,5), (2,4,3,5), (2,5,4,3), (2,5,3), (2,5,4), (2,5), (2,5,3,4), (2,5)(3,4), (1,2), (1,2)(4,5), (1,2)(3,4), (1,2)(3,4,5), (1,2)(3,5,4), (1,2)(3,5), (1,2,3), (1,2,3)(4,5), (1,2,3,4), (1,2,3,4,5), (1,2,3,5,4), (1,2,3,5), (1,2,4,3), (1,2,4,5,3), (1,2,4), (1,2,4,5), (1,2,4)(3,5), (1,2,4,3,5), (1,2,5,4,3), (1,2,5,3), (1,2,5,4), (1,2,5), (1,2,5,3,4), (1,2,5)(3,4), (1,3,2), (1,3,2)(4,5), (1,3,4,2), (1,3,4,5,2), (1,3,5,4,2), (1,3,5,2), (1,3), (1,3)(4,5), (1,3,4), (1,3,4,5), (1,3,5,4), (1,3,5), (1,3)(2,4), (1,3)(2,4,5), (1,3,2,4), (1,3,2,4,5), (1,3,5,2,4), (1,3,5)(2,4), (1,3)(2,5,4), (1,3)(2,5), (1,3,2,5,4), (1,3,2,5), (1,3,4)(2,5), (1,3,4,2,5), (1,4,3,2), (1,4,5,3,2), (1,4,2), (1,4,5,2), (1,4,2)(3,5), (1,4,3,5,2), (1,4,3), (1,4,5,3), (1,4), (1,4,5), (1,4)(3,5), (1,4,3,5), (1,4,2,3), (1,4,5,2,3), (1,4)(2,3), (1,4,5)(2,3), (1,4)(2,3,5), (1,4,2,3,5), (1,4,2,5,3), (1,4,3)(2,5), (1,4)(2,5,3), (1,4,3,2,5), (1,4)(2,5), (1,4,2,5), (1,5,4,3,2), (1,5,3,2), (1,5,4,2), (1,5,2), (1,5,3,4,2), (1,5,2)(3,4), (1,5,4,3), (1,5,3), (1,5,4), (1,5), (1,5,3,4), (1,5)(3,4), (1,5,4,2,3), (1,5,2,3), (1,5,4)(2,3), (1,5)(2,3), (1,5,2,3,4), (1,5)(2,3,4), (1,5,3)(2,4), (1,5,2,4,3), (1,5,3,2,4), (1,5)(2,4,3), (1,5,2,4), (1,5)(2,4)]
Як видно із списку, перестановки у Sage відбиваються у циклічному записі. Можна бачити, що порожні дужки () позначають тотожну перестановку (одиничний елемент). Створимо тотожну перестановку і випадковий елемент групи наступним чином.
sage: id = S5.identity()
()
sage: S5.random_element()
(1,2)(3,4)
sage: r= S5.random_element(), r
(1,3,4)(2,5)
Як можна побачити, послідовний виклик випадкового елемента щоразу повертає інший елемент групи. Можна також виразити елемент  у вигляді функції, по порядку виводячи образи
у вигляді функції, по порядку виводячи образи 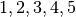 .
.
sage: r.list()
[3,5,4,1,2]
Сконструювати конкретний елемент з 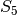 можна, перетворюючи представлену у циклічному запису перестановку у
можна, перетворюючи представлену у циклічному запису перестановку у 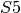 . Для коректної обробки входу у Sage треба взяти добуток циклів у лапки.
. Для коректної обробки входу у Sage треба взяти добуток циклів у лапки.
sage: r = S5('(1,3)(2,4)'); r
(1,3)(2,4)
sage: s = S5('(1,4,3,2)'); s
(1,4,3,2)
Можна також сконструювати елемент 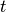 за допомогою списку образів, які він має як функція.
за допомогою списку образів, які він має як функція.
sage: t = S5([1,5,4,3,2]); t
(2,5)(3,4)
Добуток циклів береться у напрямку зліва направо. Зрозуміло, що він не є комутативним.
sage: s*t
(1,4,2,3)
sage: t*s
(1,2,4,3)
sage: id*s
Обчислимо порядок елемента за допомогою методу об’єкта order() та перевіримо правильність результату безпосередньо.
sage: r.order()
2
sage: r*r
()
sage: s.order()
4
sage: s*s
(1,3)(2,4)
sage: s*s*s*s
()
Експонентою групи називається найменший спільний множник порядків елементів.
sage: S5.exponent()
60
Метод sign() використовується для обчислення знаку перестановки, що показує, чи можна записати перестановку у вигляді парного чи непарного числа перестановок.
sage: S5('(2,3,4)').sign()
1
sage: S5('(4,5)').sign()
-1
Кожна симетрична група 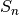 є підгрупою
є підгрупою 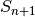 .
.
sage: S4 = SymmetricGroup(4)
sage: S4.is_subgroup(S5)
True
Підгрупу, що генерується з списку елементів, можна побудувати за допомогою методу subgroup().
sage: H = S5.subgroup([r,s])
sage: H
Subgroup of SymmetricGroup(5) generated by [(1,3)(2,4), (1,4,3,2)]
sage: H.list()
[(), (1,2,3,4), (1,3)(2,4), (1,4,3,2)]
За допомогою відповідних методів перевіримо, що щойно створена підгрупа має певні властивості. Ввід H.is() <tab> дає список деяких властивостей, які треба перевірити.
sage: H.is_abelian()
True
sage: H.is_cyclic()
True
Елементи, використані для побудови підгрупи, було отримано за допомогою методу gens(). Sage не може гарантувати, що ми виберемо саме мінімальний породжувальний набір, але це можна спробувати зробити за допомогою gens_small().
sage: H.gens()
[(1,3)(2,4), (1,4,3,2)]
sage: H.gens_small()
[(1,4,3,2)]
Корисним інструментом для вивчення структури групи є її таблиця множення, яку ще називають таблицею Келі. Викличемо метод для групи cayley_table() (інша назва команди multiplication_table()). По замовчуванню елементи групи представлені літерами (у тому порядку, у якому вони з’являються у виводі list()).
sage: S3 = SymmetricGroup(3)
sage: S3.cayley_table()
* a b c d e f
+-----------
a| a b c d e f
b| b a d c f e
c| c e a f b d
d| d f b e a c
e| e c f a d b
f| f d e b c a
sage: S3.list()
[(), (2,3), (1,2), (1,2,3), (1,3,2), (1,3)]
Можна також використовувати елементи групи самі по собі, або присвоїти їм імена. Ми присвоїмо імена елементам групи, виходячи з симетрії трикутника: u_i() для i() і r^1, r^2() для поворотів.
sage: S3.cayley_table(names='elements')
* | () (2,3) (1,2) (1,2,3) (1,3,2) (1,3)
-------------------------------------------------
() | () (2,3) (1,2) (1,2,3) (1,3,2) (1,3)
(2,3) | (2,3) () (1,2,3) (1,2) (1,3) (1,3,2)
(1,2) | (1,2) (1,3,2) () (1,3) (2,3) (1,2,3)
(1,2,3) | (1,2,3) (1,3) (2,3) (1,3,2) () (1,2)
(1,3,2) | (1,3,2) (1,2) (1,3) () (1,2,3) (2,3)
(1,3) | (1,3) (1,2,3) (1,3,2) (2,3) (1,2) ()
sage: S3.cayley_table(names=['id','u1','u3','r1','r2','u2'])
* id u1 u3 r1 r2 u2
+------------------
id| id u1 u3 r1 r2 u2
u1| u1 id r1 u3 u2 r2
u3| u3 r2 id u2 u1 r1
r1| r1 u2 u1 r2 id u3
r2| r2 u3 u2 id r1 u1
u2| u2 r1 r2 u1 u3 id
Загальні групи перестановок¶
Група перестановок - це підгрупа деякої симетричної групи. Можна побудувати групу перестановок безпосередньо, без відсилання до цілої симетричної групи, задавши список перестановок як аргумент команди PermutationGroup.
sage: r = '(1,3)(2,4)(5)'
sage: s = '(1,3,2)'
sage: K = PermutationGroup([r,s])
sage: K
Permutation Group with generators [(1,3,2), (1,3)(2,4)]
sage: K.order()
12
Декілька важливих груп перестановок можна побудувати безпосередньо. Тут наводимо найпростіші з них.
sage: K= KleinFourGroup(); K
The Klein 4 group of order 4, as a permutation group
sage: K.list()
[(), (3,4), (1,2), (1,2)(3,4)]
sage: Q= QuaternionGroup(); Q.list()
[(), (1,2,3,4)(5,6,7,8), (1,3)(2,4)(5,7)(6,8),
(1,4,3,2)(5,8,7,6), (1,5,3,7)(2,8,4,6), (1,6,3,8)(2,5,4,7),
(1,7,3,5)(2,6,4,8), (1,8,3,6)(2,7,4,5)]
sage: [x.order() for x in Q]
[1, 4, 2, 4, 4, 4, 4, 4]
Існує кілька класів груп перестановок. Клас CyclicPermutationGroup за 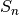 генерується за допомогою циклу
генерується за допомогою циклу 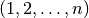 . Клас
. Клас DihedralGroup за 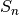 - це симетрії правильного
- це симетрії правильного 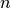 -гону із послідовною нумерацією вершин від 1 до
-гону із послідовною нумерацією вершин від 1 до 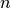 за годинниковою стрілкою. Він генерується операціями повороту
за годинниковою стрілкою. Він генерується операціями повороту  та відбиття. За допомогою методу
та відбиття. За допомогою методу gens() можна продивитись список генерувальних перетворень. Множина всіх парних перестановок, тобто перестановок із додатнім знаком— це підгрупа 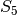 , що отримується за допомогою команди
, що отримується за допомогою команди AlternatingGroup.
sage: C = CyclicPermutationGroup(4); C
Cyclic group of order 4 as a permutation group
sage: C.list()
[(), (1,2,3,4), (1,3)(2,4), (1,4,3,2)]
sage: D = DihedralGroup(4); D
Dihedral group of order 8 as a permutation group
sage: D.list()
[(), (2,4), (1,2)(3,4), (1,2,3,4), (1,3), (1,3)(2,4), (1,4,3,2),
(1,4)(2,3)]
sage: D.gens()
[(1,2,3,4), (1,4)(2,3)]
sage: A = AlternatingGroup(4); A
Alternating group of order 4!/2 as a permutation group
sage: A.cardinality()
12
Інша вбудована група - це DiCyclicGroup (див. статтю групові властивості). Перевіримо, що 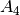 неізоморфна по відношенню до діциклічної групи з тією самою кількістю елементів.
неізоморфна по відношенню до діциклічної групи з тією самою кількістю елементів.
sage: B = DiCyclicGroup(3); B
Diyclic group of order 12 as a permutation group
sage: B.list()
[(), (5,6,7), (5,7,6), (1,2)(3,4), (1,2)(3,4)(5,6,7), (1,2)(3,4)(5,7,6), (1,3,2,4)(6,7), (1,3,2,4)(5,6), (1,3,2,4)(5,7), (1,4,2,3)(6,7), (1,4,2,3)(5,6), (1,4,2,3)(5,7)]
sage: A.is_isomorphic(B)
False
Для будь-якої групи перестановок можна порахувати її потужність, вивести список елементів, обрахувати порядки елементів і т.д. За допомогою процедур властивостей списку python (див. Списки) можна створити список елементів із певними властивостями. У даному випадку ми збудуємо список елементів порядку 2.
sage: S5 = SymmetricGroup(5)
sage: T = [s for s in S5 if s.order() == 2 ]; T
[(4,5), (3,4), (3,5), (2,3), (2,3)(4,5), (2,4), (2,4)(3,5), (2,5), (2,5)(3,4), (1,2), (1,2)(4,5), (1,2)(3,4), (1,2)(3,5), (1,3), (1,3)(4,5), (1,3)(2,4), (1,3)(2,5), (1,4), (1,4)(3,5), (1,4)(2,3), (1,4)(2,5), (1,5), (1,5)(3,4), (1,5)(2,3), (1,5)(2,4)]
Далі побудуємо групу перестановок 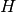 та виведемо її елементи. Ця група
та виведемо її елементи. Ця група 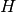 має елементи, відмінні від
має елементи, відмінні від DihedralGroup(5), але є ізоморфна до неї.
sage: H= PermutationGroup(['(1,5),(3,4)', '(1,2,5,4,3)']); H
Subgroup of SymmetricGroup(5) generated by [(1,2,5,4,3), (1,5)(3,4)]
sage: H.list()
[(), (2,3)(4,5), (1,2)(3,5), (1,2,5,4,3), (1,3,4,5,2), (1,3)(2,4), (1,4,2,3,5), (1,4)(2,5), (1,5)(3,4), (1,5,3,2,4)]
sage: H.order()
10
sage: D = DihedralGroup(5)
sage: D
Dihedral group of order 10 as a permutation group
sage: D.list()
[(), (2,5)(3,4), (1,2)(3,5), (1,2,3,4,5), (1,3)(4,5), (1,3,5,2,4), (1,4)(2,3), (1,4,2,5,3), (1,5,4,3,2), (1,5)(2,4)]
sage: H == D
False
sage: H.is_isomorphic(D)
True
Як і у випадку симетричних груп, можна скерувати список елементів групи до методу subgroup() і створити підгрупу будь-якої групи перестановок.
Список усіх підгруп групи перестановок отримаємо за допомогою методу subgroups(). Він повертає список, нульовий елемент якого є тривіальна підгрупа.
sage: D = DihedralGroup(4)
sage: L = D.subgroups(); L
[Permutation Group with generators [()], Permutation Group with generators [(1,3)(2,4)], Permutation Group with generators [(2,4)], Permutation Group with generators [(1,3)], Permutation Group with generators [(1,2)(3,4)], Permutation Group with generators [(1,4)(2,3)], Permutation Group with generators [(2,4), (1,3)(2,4)], Permutation Group with generators [(1,2,3,4), (1,3)(2,4)], Permutation Group with generators [(1,2)(3,4), (1,3)(2,4)], Permutation Group with generators [(2,4), (1,2,3,4), (1,3)(2,4)]]
Об’єднання двох підгруп 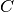 та
та 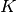 є групою, що згенерована об’єднанням цих підгруп. Об’єднання
є групою, що згенерована об’єднанням цих підгруп. Об’єднання 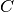 та
та 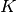 дістаємо”додаванням” відповідних списків. У прикладі далі видно, що група циклічних перестановок, згенерована
дістаємо”додаванням” відповідних списків. У прикладі далі видно, що група циклічних перестановок, згенерована 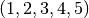 та 4-групою Клейна породжують повністю симетричну групу
та 4-групою Клейна породжують повністю симетричну групу 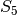 . Відмітимо, що 4-група Клейна є підгрупою
. Відмітимо, що 4-група Клейна є підгрупою 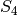 , яка сама є підгрупою
, яка сама є підгрупою 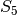 .
.
sage: K = KleinFourGroup(); K.list()
[(), (3,4), (1,2), (1,2)(3,4)]
sage: C = CyclicPermutationGroup(5)
sage: CjK = PermutationGroup(C.list()+K.list() )
Permutation Group with generators [(), (3,4), (1,2), (1,2)(3,4), (1,2,3,4,5), (1,3,5,2,4), (1,4,2,5,3), (1,5,4,3,2)]
sage: CjK.gens_small(); CjK.cardinality()
[(1,2)(3,5,4), (1,4,5,3)]
120
sage: CjK == SymmetricGroup(5)
True
Централізатор елемента  (підгрупа елементів, що комутують із
(підгрупа елементів, що комутують із  ) та центр групи будуємо в інтуїтивно очікуваний спосіб.
) та центр групи будуємо в інтуїтивно очікуваний спосіб.
sage: D.center()
Subgroup of (Dihedral group of order 8 as a permutation group) generated by [(1,3)(2,4)]
sage: D.centralizer(D('(1,3)(2,4)'))
Subgroup of (Dihedral group of order 8 as a permutation group) generated by [(1,2,3,4), (1,4)(2,3)]
Фактори груп перестановок¶
У цьому розділі розглянемо нормальні підгрупи і фактори груп за нормальною підгрупою. Спочатку звернемося до суміжних класів і спряження.
Знакозмінна група 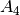 має підгрупу, ізоморфну групі Клейна 4, яка є нормальною.
має підгрупу, ізоморфну групі Клейна 4, яка є нормальною.
sage: A4 = AlternatingGroup(4)
sage: g1 = A4('(1,4)(3,2)') ; g2 = A4('(2,4)(1,3)')
sage: H = A4.subgroup([g1,g2]);
sage: H.is_normal(A4); H.is_isomorphic(KleinFourGroup())
True
True
Порівняймо лівий та правий суміжні класи 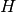 у
у 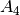 .
.
sage: Hr = A4.cosets(H, side = 'right')
sage: Hl = A4.cosets(H, side = 'left')
sage: Hr; Hl
[[(), (1,2)(3,4), (1,3)(2,4), (1,4)(2,3)], [(2,3,4), (1,3,2), (1,4,3), (1,2,4)], [(2,4,3), (1,4,2), (1,2,3), (1,3,4)]]
[[(), (1,2)(3,4), (1,3)(2,4), (1,4)(2,3)], [(2,3,4), (1,2,4), (1,3,2), (1,4,3)], [(2,4,3), (1,2,3), (1,3,4), (1,4,2)]]
sage: Hr == Hl
False
Можна переконатись, що вони рівні, але Sage порівнює кожен суміжний клас як списки, але два останні суміжні класи перераховано не у тому самому порядку. Щоб поправити це, використаємо sorted() для сортування елементів у кожній множині. У цьому прикладі нам пощастило з тим, що самі суміжні класи перераховано у тому самому порядку. Інакше треба було б застосувати sorted() до двох списків суміжних класів.
sage: Hr_sorted = [sorted(S) for S in Hr]
sage: Hl_sorted = [sorted(S) for S in Hl]
sage: Hr_sorted == Hl_sorted
True
Спряжений за  до елемента
до елемента  є елемент
є елемент 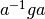 . Множина всіх спряжених до
. Множина всіх спряжених до  при зміні
при зміні  - це клас спряженості
- це клас спряженості  . Далі ми створюємо 3-цикл та обраховуємо його клас спряженості у
. Далі ми створюємо 3-цикл та обраховуємо його клас спряженості у 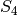 і потім у
і потім у 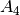 . Цей приклад показує, як два елементи можуть бути спряженими у
. Цей приклад показує, як два елементи можуть бути спряженими у 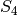 , але не у:math:A_4.
, але не у:math:A_4.
sage: S4 = SymmetricGroup(4)
sage: A4 = AlternatingGroup(4)
sage: g = S4('(1,3,4)')
sage: Set([a^(-1)*g*a for a in A4])
{(1,3,4), (1,4,2), (1,2,3), (2,4,3)}
sage: Set([a^(-1)*g*a for a in S4])
{(1,2,3), (1,3,4), (2,3,4), (2,4,3), (1,4,3), (1,2,4), (1,3,2), (1,4,2)}
Метод conjugacy_class_representatives() вибирає по одному елементу з кожного класу спряженості. Зверніть увагу, що для 3-циклу є два класи у 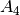 , і тільки один - у
, і тільки один - у 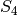 .
.
sage: S4.conjugacy_classes_representatives()
[(), (1,2), (1,2)(3,4), (1,2,3), (1,2,3,4)]
sage: A4.conjugacy_classes_representatives()
[(), (1,2)(3,4), (1,2,3), (1,2,4)]
Спряженою за  до підгрупи
до підгрупи 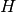 є група
є група 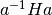 (ще раз пригадаємо, що множення відбувається зліва направо). Охоплювальні групи
(ще раз пригадаємо, що множення відбувається зліва направо). Охоплювальні групи  та
та 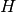 вказувати немає необхідності; Sage розглядає їх усередині симетричної групи, що містить усі релевантні цілі числа.
вказувати немає необхідності; Sage розглядає їх усередині симетричної групи, що містить усі релевантні цілі числа.
sage: H = CyclicPermutationGroup(4)
sage: K = H.conjugate(PermutationGroupElement('(3,5)')); K
Permutation Group with generators [(1,2,5,4)]
Нормалізатор 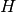 у
у 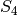 - це підгрупа елементів
- це підгрупа елементів 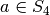 , така, що
, така, що 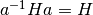 .
.
sage: S4.normalizer(H)
Permutation Group with generators [(2,4), (1,2,3,4), (1,3)(2,4)]
sage: H1 = H.conjugate(PermutationGroupElement('(2,4)')); H1
Permutation Group with generators [(1,4,3,2)]
sage: H1 ==H
True
Sage може обчислити всі нормальні підгрупи групи  . Перевіримо, що
. Перевіримо, що 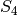 має дві нетривіальні нормальні підгрупи - знакозмінну групу та групу, ізоморфну до 4-групи Клейна (але не рівну 4-групі Клейна, стандартно визначеній у Sage).
має дві нетривіальні нормальні підгрупи - знакозмінну групу та групу, ізоморфну до 4-групи Клейна (але не рівну 4-групі Клейна, стандартно визначеній у Sage).
sage: S4 = SymmetricGroup(4)
sage: S4norms = S4.normal_subgroups(); S4norms
[Permutation Group with generators [()], Permutation Group with generators [(1,3)(2,4), (1,4)(2,3)], Permutation Group with generators [(2,4,3), (1,3)(2,4), (1,4)(2,3)], Permutation Group with generators [(1,2), (1,2,3,4)]]
sage: K = S4norms[1]; K==KleiFourGroup()
False
sage: K.is_isomorphic(KleinFourGroup())
True
sage: A = S4norms[2]; A == AlternatingGroup(4)
True
Можна також обчислити дільник  за нормальними підгрупами
за нормальними підгрупами 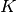 та
та  з попереднього прикладу. Як і слід було очікувати,
з попереднього прикладу. Як і слід було очікувати, 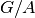 ізоморфна до
ізоморфна до 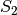 . Оскільки
. Оскільки  містить 24 елементи, а
містить 24 елементи, а 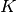 - 4 елементи, то дільник має 6 елементів. Можна перевірити, що він ізоморфний до
- 4 елементи, то дільник має 6 елементів. Можна перевірити, що він ізоморфний до 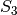 .
.
sage: G.quotient(A)
Permutation Group with generators [(1,2)]
sage: H = G.quotient(K); H
Permutation Group with generators [(1,2)(3,6)(4,5), (1,3,5)(2,4,6)]
sage: H.is_isomorphic(SymmetricGroup(3))
True
Sage також може обчислити нормалізатор підгрупи 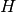 групи
групи  , який є найбільшою підгрупою
, який є найбільшою підгрупою  , що містить
, що містить 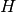 , у яких
, у яких 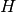 є нормальною. Обчислимо нормалізатор циклічної групи перестановок
є нормальною. Обчислимо нормалізатор циклічної групи перестановок 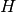 , створеної над
, створеної над 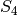 . Дістанемо дігедральну групу
. Дістанемо дігедральну групу 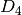 . Якщо використати інший 4-цикл, результівна група була б ізоморфною, але не рівною до
. Якщо використати інший 4-цикл, результівна група була б ізоморфною, але не рівною до 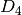 .
.
sage: G.normalizer(H).cardinality()
8
sage: HK.normalizer(H)== DihedralGroup(4)
True
Для деяких груп список їх підгруп може бути досить великим. Для кращого розуміння структури підгруп  можна обчислити по одній групі з кожного класу спряженості. У наступних обчисленнях показано, що у групи
можна обчислити по одній групі з кожного класу спряженості. У наступних обчисленнях показано, що у групи 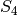 є 30 підгруп, але з точністю до спряженості - тільки 11. Кожна інша підгрупа не тільки є ізоморфною до однієї з цих 11, які можна отримати операцією
є 30 підгруп, але з точністю до спряженості - тільки 11. Кожна інша підгрупа не тільки є ізоморфною до однієї з цих 11, які можна отримати операцією conjugacy_classes_subgroups(), але також ізоморфна за спряженістю з певним елементом  .
.
sage: G
Symmetric group of order 4! as a permutation group
sage: G.subgroups()
[Permutation Group with generators [()], Permutation Group with generators [(1,2)(3,4)], Permutation Group with generators [(1,3)(2,4)], Permutation Group with generators [(1,4)(2,3)], Permutation Group with generators [(3,4)], Permutation Group with generators [(2,3)], Permutation Group with generators [(2,4)], Permutation Group with generators [(1,2)], Permutation Group with generators [(1,3)], Permutation Group with generators [(1,4)], Permutation Group with generators [(2,4,3)], Permutation Group with generators [(1,2,3)], Permutation Group with generators [(1,4,2)], Permutation Group with generators [(1,3,4)], Permutation Group with generators [(1,4)(2,3), (1,3)(2,4)], Permutation Group with generators [(1,2)(3,4), (3,4)], Permutation Group with generators [(1,4)(2,3), (2,3)], Permutation Group with generators [(1,3)(2,4), (2,4)], Permutation Group with generators [(1,2)(3,4), (1,3,2,4)], Permutation Group with generators [(1,3)(2,4), (1,4,3,2)], Permutation Group with generators [(1,4)(2,3), (1,2,4,3)], Permutation Group with generators [(3,4), (2,4,3)], Permutation Group with generators [(3,4), (1,3,4)], Permutation Group with generators [(1,2), (1,2,3)], Permutation Group with generators [(1,2), (1,4,2)], Permutation Group with generators [(1,3)(2,4), (1,4)(2,3), (1,2)], Permutation Group with generators [(1,2)(3,4), (1,3)(2,4), (1,4)], Permutation Group with generators [(1,4)(2,3), (1,2)(3,4), (1,3)], Permutation Group with generators [(1,3)(2,4), (1,4)(2,3), (2,4,3)], Permutation Group with generators [(1,3)(2,4), (1,4)(2,3), (2,4,3), (1,2)]]
sage: len(G.subgroups())
30
sage: G.conjugacy_classes_subgroups()
[Permutation Group with generators [()], Permutation Group with generators [(1,3)(2,4)], Permutation Group with generators [(3,4)], Permutation Group with generators [(2,4,3)], Permutation Group with generators [(1,4)(2,3), (1,3)(2,4)], Permutation Group with generators [(1,2)(3,4), (3,4)], Permutation Group with generators [(1,2)(3,4), (1,3,2,4)], Permutation Group with generators [(3,4), (2,4,3)], Permutation Group with generators [(1,3)(2,4), (1,4)(2,3), (1,2)], Permutation Group with generators [(1,3)(2,4), (1,4)(2,3), (2,4,3)], Permutation Group with generators [(1,3)(2,4), (1,4)(2,3), (2,4,3), (1,2)]]
sage: len(G.conjugacy_classes_subgroups())
11
Вправи
Знайти дві підгрупи
, спряжені у
, але неспряжені у
.
Гомоморфізми груп перестановок¶
Для побудови гомоморфізму між двома групами перестановок використаємо команду PermutationGroupMorphism(). Для прикладу застосуємо її для двох ізоморфних груп, побудованих раніше.
sage: G = SymmetricGroup(5)
sage: r = G('(1,2,5,4,3)')
sage: s = G('(1,5),(3,4)')
sage: H = G.subgroup([r,s])
sage: H
Subgroup of SymmetricGroup(5) generated by [(1,2,5,4,3), (1,5)(3,4)]
sage: D = DihedralGroup(5)
sage: D
Dihedral group of order 10 as a permutation group
Гомоморфізм між ними будується при вказанні асоціації між генераторами однієї групи до генераторів іншої. Продивитися їх можна за допомогою методу gens(), що містять групи
sage: H.gens()
[(1,2,5,4,3), (1,5)(3,4)]
sage: D.gens()
[(1,2,3,4,5), (1,5)(2,4)]
Збудуємо гомоморфізм 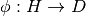 , що перетворює
, що перетворює 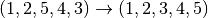 та
та 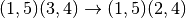 наступним чином:
наступним чином:
sage: phi = PermutationGroupMorphism(H,D,H.gens(), D.gens())
sage: phi
Homomorphism : Permutation Group with generators [(1,2,5,4,3), (1,5)(3,4)] --> Dihedral group of order 10 as a permutation group
Цей гомоморфізм можна застосувати так само, як і будь-яку функцію, викликаючи її:
sage: phi( '(2,3)(4,5)')
(1,3)(4,5)
sage: phi( '(1,5,3,2,4)')
(1,3,5,2,4)
sage: phi('(1,5)')
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
...
AttributeError: 'str' object has no attribute '_gap_init_'
Тут ми дістаємо AttributeError, оскільки перестановка 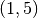 не знаходиться в області
не знаходиться в області phi().
Операція гомоморфізму також має у собі кілька корисних методів, з яких найбільш застосованим є метод kernel(), що показує ядро гомоморфізму. Оскільки гомоморфізм є ін’єкцією, ядро є тривіальною групою:
sage: phi.kernel()
Permutation Group with generators [()]
Прямий добуток двох груп перестановок не дає групу перестановок, але приводить до більшої симетричної групи. Вихід операції - список довжини 5, що складається з прямого добутку та чотирьох гомоморфізмів. Перші два гомоморфізми - це природні гомоморфізми від кожного множника в добутку. Наступні два гомоморфізми - це натуральні проекції від добутку на кожний множник.
sage: C4 = CyclicPermutationGroup(4)
sage: C3 = CyclicPermutationGroup(3)
sage: C4xC3 = C4.direct_product(C3); C4xC3
(Permutation Group with generators [(5,6,7), (1,2,3,4)], Permutation group morphism:
From: Cyclic group of order 4 as a permutation group
To: Permutation Group with generators [(5,6,7), (1,2,3,4)]
Defn: Embedding( Group( [ (1,2,3,4), (5,6,7) ] ), 1 ), Permutation group morphism:
From: Cyclic group of order 3 as a permutation group
To: Permutation Group with generators [(5,6,7), (1,2,3,4)]
Defn: Embedding( Group( [ (1,2,3,4), (5,6,7) ] ), 2 ), Permutation group morphism:
From: Permutation Group with generators [(5,6,7), (1,2,3,4)]
To: Cyclic group of order 4 as a permutation group
Defn: Projection( Group( [ (1,2,3,4), (5,6,7) ] ), 1 ), Permutation group morphism:
From: Permutation Group with generators [(5,6,7), (1,2,3,4)]
To: Cyclic group of order 3 as a permutation group
Defn: Projection( Group( [ (1,2,3,4), (5,6,7) ] ), 2 ))
Якщо потрібна саме група прямого добутку, необхідно вибрати нульовий елемент від списку прямого добутку.
sage: C4xC3[0]
Permutation Group with generators [(1,2,3,4), (5,6,7)]
Вправи
Існує гомоморфізм від діциклічної групи із індексом
до дігедральної групи із індексом
. Побудуємо його і знайдемо ядро.
Матричні групи¶
Допоможіть написати цей розділ!
Абелеві групи¶
Допоможіть написати цей розділ!
Лінійна алгебра¶
Вектори і матриці¶
Для побудови вектору використовується команда vector() із списком аргументів. Звичайним способом обчислюються скалярні кратні (добутки вектору та скаляру) та внутрішні добутки. Як і у списках, нумерація компонентів векторів починається із  .
.
sage: v= vector([1,2,3,4])
sage: v[0]
1
sage: v[4]
ERROR: An unexpected error occurred while tokenizing input
Арифметичні дії із векторами відбуваються так, як можна інтуїтивно очікувати. При спробі додавання двох векторів із різними довжинами генерується помилка.
sage: 7*v
(7, 14, 21, 28)
sage: v + vector([2,1,4,5])
(3, 3, 7, 9)
sage: v*v
sage: v + vector([2,1,4])
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
/Users/mosullivan/Work/Sage/Tutorial/sdsu-sage-tutorial/<ipython console> in <module>()
/Applications/sage/local/lib/python2.6/site-packages/sage/structure/element.so in sage.structure.element.ModuleElement.__add__ (sage/structure/element.c:7627)()
/Applications/sage/local/lib/python2.6/site-packages/sage/structure/coerce.so in sage.structure.coerce.CoercionModel_cache_maps.bin_op (sage/structure/coerce.c:6995)()
TypeError: unsupported operand parent(s) for '+': 'Ambient free module of rank 4 over the principal ideal domain Integer Ring' and 'Ambient free module of rank 3 over the principal ideal domain Integer Ring'
Матриця будується за допомогою команди matrix() із аргументами - списком рядків матриці.
sage: matrix([[1,2],[3,4]])
[1 2]
[3 4]
Також можна задати матрицю, вказуючи усі її координати та розмірність. Наступна команда дає матрицю із 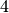 рядками та
рядками та 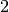 стовпчиками.
стовпчиками.
sage: matrix(4,2, [1,2,3,4,5,6,7,8])
[1 2]
[3 4]
[5 6]
[7 8]
Якщо треба збудувати квадратну матрицю, аргумент кількості стовпчиків можна опустити.
sage: matrix(2,[1,2,3,4])
[1 2]
[3 4]
За замовчуванням Sage будує матриці над найменшою генеральною сукупністю, що містить їх координати.
sage: parent(matrix(2,[1,2,3,4]))
Full MatrixSpace of 2 by 2 dense matrices over Integer Ring
sage: parent(matrix(2,[1,2/1,3,4]))
Full MatrixSpace of 2 by 2 dense matrices over Rational Field
sage: parent(matrix(2,[x,x^2,x-1,x^3])
Full MatrixSpace of 2 by 2 dense matrices over Symbolic Ring
Можна визначити генеральну сукупність для координат матриці чи вектора, задаючи її як додатковий аргумент.
sage: matrix(QQ,2,[1.1,1.2,1.3,1.4])
[11/10 6/5]
[13/10 7/5]
У Sage передбачено короткі команди для побудови деяких поширених типів матриць. Так, для побудови одиничної матриці можна використати функцію identity_matrix().
sage: identity_matrix(3)
[1 0 0]
[0 1 0]
[0 0 1]
Нульова матриця будується функцією zero_matrix() або звичайною функцією конструювання матриці, але без списку значень як аргументу.
sage: zero_matrix(2,2)
[0 0]
[0 0]
sage: matrix(2)
[0 0]
[0 0]
sage: matrix(2,3)
[0 0 0]
[0 0 0]
Зверніть увагу, що для функції zero_matrix() потрібно задати як аргументи два цілі числа.
Вправи
Побудувати у Sage вектор
Побудувати у Sage наступну матрицю над раціональними числами.
Побудувати одиничну матрицю 10x10.
Побудувати нульову матрицю 20x10.
Матрична арифметика¶
Необхідно знати розділ Вектори і матриці.
Для операцій додавання, віднімання, множення та піднесення матриць до ступеня використовуються оператори +, -, * та ^.
sage: A=matrix(2,[1,1,0,1])
sage: B=matrix(2,[1,0,1,1])
sage: A+B
[2 1]
[1 2]
sage: A*B
[2 1]
[1 1]
sage: B*A
[1 1]
[1 2]
sage: A-B
[ 0 1]
[-1 0]
sage: A^3
[1 3]
[0 1]
Обернену матрицю можна обчислити за допомогою піднесення вихідної матриці до ступеня 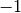 .
.
sage: A^-1
[ 1 -1]
[ 0 1]
Якщо оберненої матриці не існує, Sage видає помилку ZeroDivisionError.
sage: A = matrix([[4,2],[8,4]])
sage: A^-1
---------------------------------------------------------------------------
ZeroDivisionError Traceback (most recent call last)
... (Long error message)
ZeroDivisionError: input matrix must be nonsingular
При перемноженні векторів та матриць вектори можна розглядати і як рядки, і як стовпчики. Тому можна помножити 3-компонентний вектор на матрицю 3×n справа, або на матрицю n×3 зліва.
sage: x = vector([12,3,3])
sage: x
(12, 3, 3)
sage: A
[1 2 3]
[4 5 6]
sage: A*x
(27, 81)
sage: B = transpose(A)
sage: B
[1 4]
[2 5]
[3 6]
sage: x*B
(27, 81)
Для обчислення визначника квадратної матриці використовується метод det().
sage: A= matrix([[-1/2,0,-1],[0,-2,2],[1,0,-1/2]]); A
[-1/2 0 -1]
[ 0 -2 2]
[ 1 0 -1/2]
sage: A.det()
-5/2
Метод is_invertible() дозволяє визначити, чи є матриця оборотною.
sage: A=matrix(2,[1,1,0,1])
sage: A.is_invertible()
True
sage: A.det()
1
Властивість оборотності матриці залежить від кільця або поля, над яким вона визначена. Наприклад:
sage: B=matrix(2,[1,2,3,4])
sage: B.is_invertible()
False
У цьому прикладі Sage приймає, що матрицю B``визначено над полем цілих, а не раціональних чисел, де вона оберненої не має. Але при заданні ``B як матриці над раціональними числами результат буде іншим.
sage: B = matrix(QQ, 2,[1,2,3,4])
sage: B
[1 2]
[3 4]
sage: B.is_invertible()
True
Якщо задати Sage команду обчислення оберненої матриці до матриці, визначеної над цілими числами, то програма за необхідності виконає автоматичне перетворення типу B до матриці над раціональними числами.
sage: B = matrix(2,[1,2,3,4])
sage: parent(B)
Full MatrixSpace of 2 by 2 dense matrices over Integer Ring
sage: B^-1
[ -2 1]
[ 3/2 -1/2]
sage: parent(B^-1)
Full MatrixSpace of 2 by 2 dense matrices over Rational Field
Вправи
Розглянемо наступні матриці:
Яка з наступних матриць є обратимою над
? А над
?
Робота із матрицями¶
Необхідно знати розділи Вектори і матриці та Матрична арифметика.
У цьому розділі ми розглянемо деякі команди для маніпуляцій із матрицями. Почнемо із визначення матриці на раціональних числах.
sage: M = matrix(QQ, [[1,2,3],[4,5,6],[7,8,9]]); M
[1 2 3]
[4 5 6]
[7 8 9]
Для отримання списку векторів-рядків і векторів-стовпчиків використовуються методи rows() та columns() відповідно.
sage: M.rows()
[(1, 2, 3), (4, 5, 6), (7, 8, 9)]
sage: M.columns()
[(1, 4, 7), (2, 5, 8), (3, 6, 9)]
У наступних прикладах показано, як можна вивести конкретний вектор-рядок чи вектор-стовпчик. Нагадаємо, що у Sage використовується правило (як і у мові Python) нумерування усіх індексів від нуля.
sage: M.row(0)
(1, 2, 3)
sage: M.row(2)
(7, 8, 9)
sage: M.column(1)
(2, 5, 8)
sage: M.column(2)
(3, 6, 9)
Можна також вивести список діагональних елементів. Для цього використовують метод diagonal().
sage: M.diagonal()
[1, 5, 9]
Sage також дозволяє побудувати нові матриці з векторів-рядків або векторів-стовпчиків.
sage: M.matrix_from_columns([0,2])
[1 3]
[4 6]
[7 9]
sage: M.matrix_from_rows([0,2])
[1 2 3]
[7 8 9]
sage: M.matrix_from_rows_and_columns([0,2],[0,2])
[1 3]
[7 9]
Відмітимо, що matrix_from_rows_and_columns() повертає перетин вказаних рядків та стовпчиків. У наведеному прикладі ми вибираємо матрицю, що складається з чотирьох ‘кутів’ нашої матриці 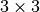 .
.
Розглянемо кілька простих операцій із рядками. Для множення рядка або стовпчика на число використовуються методи rescale_row() або rescale_column(). При цьому змінюється сама матриця.
sage: M.rescale_row(1,-1/4); M
[ 1 2 3]
[ -1 -5/4 -3/2]
[ 7 8 9]
sage: M.rescale_col(2,-1/3); M
[ 1 2 -1]
[ -1 -5/4 1/2]
[ 7 8 -3]
sage: M.rescale_row(1,-4); M
[ 1 2 -1]
[ 4 5 -2]
[ 7 8 -3]
Можна додати добуток рядка або стовпчика до іншого рядка або стовпчика. Для цього використовується метод add_multiple_of_row(). Перша команда обчислює добуток 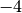 на рядок
на рядок  і додає результат до рядка
і додає результат до рядка 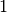 .
.
sage: M.add_multiple_of_row(1,0,-4); M
[ 1 2 -1]
[ 0 -3 2]
[ 7 8 -3]
sage: M.add_multiple_of_row(2,0,-7); M
[ 1 2 -1]
[ 0 -3 2]
[ 0 -6 4]
Такі ж операції можна провести із векторами у вигляді стовпчиків, які теж мають нульовий індекс.
sage: M.add_multiple_of_column(1,0,-2);M
[ 1 0 -1]
[ 0 -3 2]
[ 0 -6 4]
sage: M.add_multiple_of_column(2,0,1);M
[ 1 0 0]
[ 0 -3 2]
[ 0 -6 4]
За необхідності можна змінити на місці порядок рядків або стовпчиків.
sage: M.swap_rows(1,0); M
[ 0 -3 2]
[ 1 0 0]
[ 0 -6 4]
sage: M.swap_columns(0,2); M
[ 2 -3 0]
[ 0 0 1]
[ 4 -6 0]
Щоб замінити рядок або стовпчик M, треба використати метод set_row() або set_column() відповідно.
sage: M.set_column(0,[1,2,3]);M
[ 1 -3 0]
[ 2 0 1]
[ 3 -6 0]
sage: M.set_row(0,[1,2,5]);M
[ 1 2 5]
[ 2 0 1]
[ 3 -6 0]
І на кінець, якщо треба замінити цілий блок у матриці, можна використати метод set_block(), задаючи координати початку блоку, тобто його верхнього лівого кута.
sage: B = matrix(QQ,[ [1,0 ],[0,1]]); B
[1 0]
[0 1]
sage: M.set_block(1,1,B); M
[1 2 5]
[2 1 0]
[3 0 1]
Зрозуміло, якщо нам потрібна тільки ешелонована форма матриці, можна використати один з методів echelon_form() або echelonize(). Різниця між цими методами полягає у тому, що перший повертає копію матриці у ешелонованій формі без зміни вихідної матриці, а другий змінює саму матрицю.
sage: M.echelon_form()
[1 0 0]
[0 1 0]
[0 0 1]
sage: M.echelonize(); M
[ 1 0 0]
[ 0 1 0]
[ 0 0 1]
Тепер ми використаємо нарощену матрицю та ешелонну форму запису для розв’язання системи 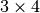 у формі
у формі 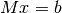 . Задамо матрицю M та вектор b
. Задамо матрицю M та вектор b
sage: M = matrix(QQ, [[2,4,6,2,4],[1,2,3,1,1],[2,4,8,0,0],[3,6,7,5,9]]); M
[2 4 6 2 4]
[1 2 3 1 1]
[2 4 8 0 0]
[3 6 7 5 9]
sage: b = vector(QQ, [56, 23, 34, 101])
Побудуємо нарощену матрицю 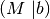 , запишемо її до змінної M_aug та обчислимо її ешелоновану форму.
, запишемо її до змінної M_aug та обчислимо її ешелоновану форму.
sage: M_aug = M.augment(b); M_aug
[ 2 4 6 2 4 56]
[ 1 2 3 1 1 23]
[ 2 4 8 0 0 34]
[ 3 6 7 5 9 101]
sage: M_aug.echelon_form()
[ 1 2 0 4 0 21]
[ 0 0 1 -1 0 -1]
[ 0 0 0 0 1 5]
[ 0 0 0 0 0 0]
З цього видно, що одновимірний простір розв’язків складається з векторів у формі 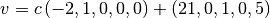 .
.
sage: M*vector([21,0,-1,0,5])
(56, 23, 34, 101)
sage M*vector([-2,1,0,0,0])
(0, 0, 0, 0)
Якщо потрібен тільки один розв’язок системи, можна застосувати метод solve_right().
sage: M.solve_right(b)
(21, 0, -1, 0, 5)
Вправи
Розглянемо матрицю.
Переведемо
у ешелоновану форму із використанням тільки описаних елементарних операцій.
За допомогою команд цього розділу переведемо матрицю зліва у матрицю, показану справа.
Простори векторів та матриць¶
Буває іноді корисно створити простір усіх матриць певної розмірності, для чого можна використати функцію MatrixSpace(). Треба визначити поле (або взагалі кажучи - будь-яке кільце), у якому існують елементи.
sage: MatrixSpace(QQ,2,3)
Full MatrixSpace of 2 by 3 dense matrices over Rational Field
При завданні кільця 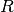 та цілого числа
та цілого числа  ми отримуємо матричне кільце
ми отримуємо матричне кільце 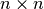 матриць на
матриць на 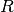 . Для побудови нульової, ідентичної матриці або матриці з заданими елементами, як показано тут, можна використати перетворення типу.
. Для побудови нульової, ідентичної матриці або матриці з заданими елементами, як показано тут, можна використати перетворення типу.
sage: Mat = MatrixSpace(ZZ,2); Mat
Full MatrixSpace of 2 by 2 dense matrices over Integer Ring
sage: Mat(1)
[1 0]
[0 1]
sage: Mat(0)
[0 0]
[0 0]
sage: Mat([1,2,3,4])
[1 2]
[3 4]
Можна обчислити асоційовані із матрицею різні простори:
sage: Mat = MatrixSpace(QQ, 3,4)
sage: A = Mat([[1,2,3,4], [1,3,4,4],[2,5,7,8]])
sage: A
[1 2 3 4]
[1 3 4 4]
[2 5 7 8]
sage: A.rank()
2
sage: A.right_kernel()
Vector space of degree 4 and dimension 2 over Rational Field
Basis matrix:
[ 1 0 0 -1/4]
[ 0 1 -1 1/4]
sage: A.left_kernel()
Vector space of degree 3 and dimension 1 over Rational Field
Basis matrix:
[ 1 1 -1]
sage: A.row_space()
Vector space of degree 4 and dimension 2 over Rational Field
Basis matrix:
[1 0 1 4]
[0 1 1 0]
Вправи
Для наступної матриці 5x3:
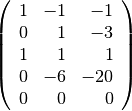
Використаємо Sage для обчислення базису для наступних просторів:
Праве і ліве ядро.
Простір рядків.
Простір колонок.
Міні-розділ: канонічна форма Жордана¶
Для будь-якого лінійного перетворення 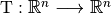 існує базис
існує базис 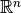 , такий, у якому матриця
, такий, у якому матриця ![\left[m\right]_{\mathcal{B}}](_images/math/dc572679cccf6c6cd31990a716f3e2e6dcdd48b6.png) буде мати майже діагональний вид. Така єдина матриця носить назву канонічної форми Жордана перетворення
буде мати майже діагональний вид. Така єдина матриця носить назву канонічної форми Жордана перетворення 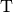 . Більш докладну інформацію можна знайти у цій статті у вікіпедії. Ми знайдемо цей базис для лінійного перетворення і розглянемо деякі інструменти, які для цього існують у Sage
. Більш докладну інформацію можна знайти у цій статті у вікіпедії. Ми знайдемо цей базис для лінійного перетворення і розглянемо деякі інструменти, які для цього існують у Sage
Почнемо із побудови у Sage матриці 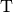 .
.
sage: T(x,y,z,t) = (2*x+y, 2*y+1, 3*z, y - z + 3*t)
Тепер використаємо стандартно упорядкований базис 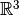 для знаходження матричної форми
для знаходження матричної форми 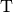 .
.
sage: T(1,0,0,0), T(0,1,0,0), T(0,0,1,0), T(0,0,0,1)
((2, 1, 0, 0), (1, 3, 0, 1), (0, 1, 3, -1), (0, 1, 0, 3))
Зверніть увагу: у Sage для побудови матриць використовуються рядки, а тому для отримання шуканої матриці слід використати функцію transpose().
sage: M = transpose(matrix([[2,1,0,0],[0,2,1,0], [0,0,3,0],[0,1,-1,3]])); M
[ 2 1 0 0]
[ 0 2 1 0]
[ 0 0 3 0]
[ 0 1 -1 3]
Після побудови матриці обчислимо її характеристичний поліном і факторизуємо його.
sage: f = M.characteristic_polynomial(); f
x^4 - 10*x^3 + 37*x^2 - 60*x + 36
sage: f.factor()
(x - 3)^2 * (x - 2)^2
У прикладі вище ми маємо два власних значення 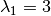 та
та 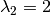 , кожне з яких має алгебраїчну кратність
, кожне з яких має алгебраїчну кратність 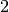 . Тепер розглянемо відповідні власні вектори. Для цього застосуємо метод
. Тепер розглянемо відповідні власні вектори. Для цього застосуємо метод eigenvectors_right().
sage: ev_M = M.eigenvectors_right(); ev_M
[(3, [
(1, 1, 1, 0),
(0, 0, 0, 1)
], 2), (2, [
(1, 0, 0, 0)
], 2)]
sage: ev_M[1][1][0]
(1, 0, 0, 0)
При цьому виводиться список (list()) упорядкованих трійок. Кожна трійка складається із власного значення, за яким іде список базисних векторів асоційованого власного простору, і потім - розмірність власного простору. Відмітимо, що власне значення 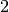 має алгебраїчну кратність
має алгебраїчну кратність 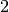 , але геометричну кратність тільки
, але геометричну кратність тільки 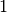 . Це означає, що нам потрібно обчислити узагальнений власний вектор для цього власного значення. Це робиться за допомогою розв’язання системи
. Це означає, що нам потрібно обчислити узагальнений власний вектор для цього власного значення. Це робиться за допомогою розв’язання системи 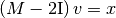 , де
, де 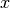 - це власний вектор
- це власний вектор  . Для розв’язання системи використаємо метод
. Для розв’язання системи використаємо метод echelon_form() для розширеної матриці.
sage: (M - 2*identity_matrix(4)).augment(ev_M[1][1][0])
[ 0 1 0 0 1]
[ 0 0 1 0 0]
[ 0 0 1 0 0]
[ 0 1 -1 1 0]
sage: _.echelon_form()
[ 0 1 0 0 1]
[ 0 0 1 0 0]
[ 0 0 0 1 -1]
[ 0 0 0 0 0]
sage: gv = vector([1,1,0,-1]); gv
(1, 1, 0, -1)
Маючи узагальнений власний вектор gv, ми тепер дістаємо правильну кількість лінійно незалежних векторів для побудови базису нашої матриці у жордановій формі. Далі ми проведемо матрицю зміни базису, що містить ці вектори як стовпчики.
sage: S = transpose( matrix( [[1,1,1,0],[0,0,0,1],[1,0,0,0],gv])); S
[ 1 0 1 1]
[ 1 0 0 1]
[ 1 0 0 0]
[ 0 1 0 -1]
Тепер обчислимо матричне представлення 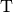 по відношенню до цього базису.
по відношенню до цього базису.
sage: S.inverse()*M*S
[3 0 0 0]
[0 3 0 0]
[0 0 2 1]
[0 0 0 2]
Це і є канонічна жорданова форма лінійного перетворення 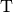 . Такого ж результату можна було досягнути і безпосередньо із використанням вбудованого методу Sage
. Такого ж результату можна було досягнути і безпосередньо із використанням вбудованого методу Sage jordan_form().
sage: M.jordan_form()
[3|0|0 0]
[-+-+---]
[0|3|0 0]
[-+-+---]
[0|0|2 1]
[0|0|0 2]
Але ж це не було б так захоплююче.
Вправи
Обчисліть жордановий базис для наступної матриці із використанням описаних у цьому розділі кроків.
Кільця¶
Поліномінальні кільця¶
У Sage поліномінальні кільця будуються дуже прозоро. Потрібно тільки вказати ім’я “невизначеної” змінної і кільце коефіцієнтів.
sage: R.<x>=PolynomialRing(ZZ)
sage: R
Univariate Polynomial Ring in x over Integer Ring
Після завдання поліномінального кільця можна побудувати поліном без будь-яких спеціальних перетворень типу.
sage: p = 2*x^2 + (1/2)*x + (3/5)
sage: parent(p)
Univariate Polynomial Ring in x over Rational Field
Хоча 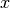 - це стандартний вибір для імені змінної, можна задати для невизначеної змінної будь-яку іншу літеру.
- це стандартний вибір для імені змінної, можна задати для невизначеної змінної будь-яку іншу літеру.
sage: R.<Y>=PolynomialRing(QQ)
sage: R
Univariate Polynomial Ring in Y over Rational Field
Поліноми із раціональними коефіцієнтами в Y - це звичайні об’єкти Sage.
sage: q = Y^4 + (1/2)*Y^3 + (1/3)*Y + (1/4)
sage: q
Y^4 + 1/2*Y^3 + 1/3*Y + 1/4
sage: parent(q)
Univariate Polynomial Ring in Y over Rational Field
Поліномінальне кільце можна визначити на будь-якому кільці чи полі.
sage: Z7=Integers(7)
sage: R.<x>=PolynomialRing(Z7); R
Univariate Polynomial Ring in x over Ring of integers modulo 7
При введенні у Sage поліному його коефіцієнти автоматично перетворюються у зазначене кільце або поле:
sage: p = 18*x^2 + 7*x + 16; p
4*x^2 + 2
sage: parent(p)
Univariate Polynomial Ring in x over Ring of integers modulo 7
Зрозуміло, це перетворення типу має бути коректно визначене:
sage: q = x^4 + (1/2)*x^3 + (1/3)*x^2 + (1/4)*x + (1/5)
---------------------------------------------------------------------------
TypeError Traceback (most recent call last) ...
TypeError: unsupported operand parent(s) for '*': 'Rational Field' and 'Univariate Polynomial Ring in x over Ring of integers modulo 7'
Слід уточнити, що Sage розширює всесвіт визначень для введеного поліному. Наприклад,при спробі задати раціональний коефіцієнт у поліномінальному кільці над  Sage перетворить цей поліном у кільце над
Sage перетворить цей поліном у кільце над 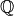
sage: S.<y>=PolynomialRing(ZZ)
sage: 1/2*y
1/2*y
sage: parent(1/2*y)
Univariate Polynomial Ring in y over Rational Field
Відмітимо, що кільце S не змінилося взагалі, як не змінилося і (1/2)*y` у всесвіті ``S, що легко можна перевірити.
sage: S
Univariate Polynomial Ring in y over Integer Ring
sage: (1/2)*y in S
False
Після побудови основні арифметичні операції над поліномами виконуються безпосередньо.
sage: R.<x>=PolynomialRing(QQ)
sage: f=x+1
sage: g=x^2+x-1
sage: h=1/2*x+3/4
sage: f+g
x^2 + 2*x
sage: g-h
x^2 + 1/2*x - 7/4
sage: f*g
x^3 + 2*x^2 - 1
sage: h^3
1/8*x^3 + 9/16*x^2 + 27/32*x + 27/64
Також елементи поліноміального кільця можна ділити, але при цьому змінюється породжувальний елемент.
sage: f/g
(x + 1)/(x^2 + x - 1)
sage: parent(f/g)
Fraction Field of Univariate Polynomial Ring in x over Rational Field
Фундаментальний атрибут поліному є його ступінь. Для її обчислення можна використати метод degree().
sage: R.<x>=PolynomialRing(QQ)
sage: (x^3+3).degree()
3
sage: R(0).degree()
-1
За узгодженням ступінь 0 позначається у Sage як -1.
Поліноміальне кільце над полем має алгоритм ділення. Так само, як і для цілих чисел, можна використати оператор // для визначення частки, а оператор % - для визначення рештки операції ділення.
sage: R.<x>=PolynomialRing(Integers(7))
sage: f=x^6+x^2+1
sage: g=x^3+x+1
sage: f // g
x^3 + 6*x + 6
sage: f % g
2*x^2 + 2*x + 2
Крім того, якщо коефіцієнти поліному належать  або
або 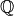 , для обчислення обох одночасно можна використати команду
, для обчислення обох одночасно можна використати команду divmod().
sage: S.<y>=PolynomialRing(QQ)
sage: a=(y+1)*(y^2+1)
sage: b=(y+1)*(y+5)
sage: a // b
y - 5
sage: a % b
26*y + 26
sage: divmod(a,b)
(y - 5, 26*y + 26)
Для поля 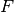 поліноміальне кільце
поліноміальне кільце ![F[x]](_images/math/7d71bb7a0516ff9c5864fd67d40e753d66e3767c.png) має алгоритм ділення, так що можна визначити єдиний найбільший спільний дільник (gcd) поліномів. Для цього використаємо команду
має алгоритм ділення, так що можна визначити єдиний найбільший спільний дільник (gcd) поліномів. Для цього використаємо команду gcd().
sage: R.<x> = PolynomialRing(QQ)
sage: p = x^4 + 2*x^3 + 2*x^2 + 2*x + 1
sage: q = x^4 - 1
sage: gcd(p,q)
x^3 + x^2 + x + 1
Найбільший спільний дільник двох цілих чисел можна представити як лінійну комбінацію двох цілих чисел, і для визначення цієї комбінації використовується розширений алгоритм Евкліда. Аналогічно найбільший спільний дільник поліномів 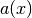 та
та 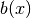 записується у формі
записується у формі 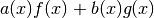 із деякими поліномами
із деякими поліномами 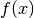 та
та 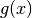 . Для визначення множників
. Для визначення множників 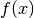 та
та 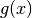 можна скористатись із команди
можна скористатись із команди xgcd().
sage: R.<x>=PolynomialRing(ZZ)
sage: a=x^4-1
sage: b=(x+1)*x
sage: xgcd(a,b)
(x + 1, -1, x^2 - x + 1)
sage: d,u,v=xgcd(a,b)
sage: a*u+b*v
x + 1
Метод is_irreducible() використовується для перевірки незвідності поліному.
sage: R.<x>=PolynomialRing(Integers(5))
sage: (x^3+x+1).is_irreducible()
True
sage: (x^3+1).is_irreducible()
False
Цей метод підходить тільки для кілець поліномів, визначених над певним полем, оскільки поліноми, визначені більш загально, можуть факторизуватись не єдиним способом.
Для знаходження факторизації поліному використовується команда factor().
sage: R.<x>=PolynomialRing(Integers(5))
sage: factor(x^3+x+1)
x^3 + x + 1
sage: factor(x^3+1)
(x + 1) * (x^2 + 4*x + 1)
У прикладі вище ми переконалися, що вираз 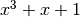 є незвідним у
є незвідним у ![\mathbb{Z}_{5}[x]](_images/math/775b601d7f8a0857dc63b845c83d4fc9e7133f6e.png) , тоді як
, тоді як 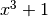 можна факторизувати, отже, він є звідним.
можна факторизувати, отже, він є звідним.
Можна також розглянути поліноми у ![R[x]](_images/math/74fc50cb9e221c8ee7b9ae8ce27089521b2de65c.png) як функції з
як функції з 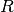 до
до 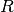 за обчисленням, тобто заміною неозначеної змінної елементом кільця коефіцієнтів. Обчислення поліномів у Sage працює, як і слід очікувати, шляхом виклику поліному як функції.
за обчисленням, тобто заміною неозначеної змінної елементом кільця коефіцієнтів. Обчислення поліномів у Sage працює, як і слід очікувати, шляхом виклику поліному як функції.
sage: R.<x>=PolynomialRing(Integers(3))
sage: f=2*x+1
sage: f(0)
1
sage: f(1)
0
sage: f(2)
2
Обчислення коренів, або нулів поліному можна провести за допомогою методу roots().
sage: ((x-1)^2*(x-2)*x^3).roots()
[(2, 1), (1, 2), (0, 3)]
При цьому у результаті Sage видає список пар 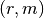 , у якому
, у якому r - це корінь, а m - його кратність. Зрозуміло, є поліноми без коренів. У такому випадку видається порожній список.
sage: (x^2+1).roots()
[]
Поліноміальні кільця із декількома змінними¶
Можна легко задати поліноміальне кільце із більше, ніж одною змінною, якщо вказати додатковий аргумент для функції PolynomialRing(), який задає кількість потрібних змінних.
sage: R.<x,y,z> = PolynomialRing(QQ, 3)
sage: p = -1/2*x - y*z - y + 8*z^2; p
-y*z + 8*z^2 - 1/2*x - y
На відміну від поліномів із однією змінною, впорядкувати члени поліному можна не одним способом. Тобто для завдання ступеня та провідного члена поліному тощо ми спочатку маємо визначити правило, що вказує, коли один член є більшим від іншого. Без додаткових аргументів Sage за замовчуванням приймає ступенево-обернено-словниковий алгоритм впорядкування, який іноді ще називають grevlex. Детальнішу інформацію щодо впорядкування мономів див. на цій сторінці у вікіпедії.
Для отримання списку мономів із ненульовими коефіцієнтами по 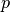 треба використати метод
треба використати метод monomials().
sage: p.monomials()
[y*z, z^2, x, y]
Ці мономи виводяться зі зменшенням порядку від старшого до молодшого згідно із правилом впорядкування членів, яке було задане при побудові кільця.
Вивести список коефіцієнтів можна, застосовуючи метод coefficients().
sage: p.coefficients()
[-1, 8, -1/2, -1]
Список коефіцієнтів виводиться у тому самому порядку, як і список мономів, визначеному раніше. Це означає, що за допомогою функції zip() можна попарно об’єднати члени обох списків, отримуючи відповідно список членів поліному.
sage: [ a*b for a,b in zip(p.coefficients(),p.monomials())]
[-y*z, 8*z^2, -1/2*x, -y]
Іноді потрібно працювати із властивостями старшого, або ведучого члена. Наступним способом можна визначити ведучий коефіцієнт, ведучий моном та ведучий член:
sage: p.lc()
-1
sage:
sage: p.lm()
y*z
sage: p.lt()
-y*z
Також за допомогою методу total_degree() можна визначити повний ступінь поліному.
sage: p.total_degree()
2
Експоненційна функція за кожною змінною у кожному члені, знову із впорядкуванням від старшого до молодшого, обчислюється методом exponents().
sage: p.exponents()
[(0, 1, 1), (0, 0, 2), (1, 0, 0), (0, 1, 0)]
Експоненту від ведучого члену можна дістати, послідовно застосовуючи два останні методи.
sage: p.lm().exponents()
[(0, 1, 1)]
Для зміни впорядкування треба перебудувати як саме кільце, так і усі використані поліноми. За допомогою наступного коду ми будуємо поліноміальне кільце зі змінними 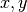 і
і  зі словниковим впорядкуванням мономів.
зі словниковим впорядкуванням мономів.
sage: R.<x,y,z> = PolynomialRing(QQ,3,order='lex')
sage: p = -1/2*x - y*z - y + 8*z^2; p
-1/2*x - y*z - y + 8*z^2
Новий спосіб впорядкування впливає на усі розглянуті методи, навіть спосіб зображення поліному у Sage.
sage: p.lm()
x
sage: p.lc()
-1/2
sage: p.lt()
-1/2*x
sage: p.monomials()
[x, y*z, y, z^2]
Відмітимо, що на впорядкування впливає порядок запису невизначених членів. У прикладі вище використовується словникове впорядкування із 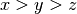 . Перевизначимо кільце зі зворотним словниковим впорядкуванням
. Перевизначимо кільце зі зворотним словниковим впорядкуванням 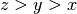 .
.
sage: R.<z,y,x> = PolynomialRing(QQ,3,order='lex')
sage: p = -1/2*x - y*z - y + 8*z^2
sage: p
8*z^2 - z*y - y - 1/2*x
sage: p.lm()
z^2
sage: p.lc()
8
sage: p.lt()
8*z^2
Знову зауважимо, що усі методи автоматично приймають новий алгоритм впорядкування.
На кінець, можна виконати приведення поліному за модулем із використанням списку поліномів за допомогою методу mod().
sage: r = -x^2 + 1/58*x*y - y + 1/2*z^2
sage: r.mod([p,q])
-238657765/29696*y^2 + 83193/14848*y*z^2 + 68345/14848*y - 1/1024*z^4 + 255/512*z^2 - 1/1024
Вправи
З’ясуйте за допомогою Sage, які з нижче наведених поліномів із раціональними коефіцієнтами є незвідними.
Зробіть факторизацію поліномів за
.
Обчисліть усі корені наступних поліномів, визначених на
. Порівняйте цей список із виразами їх факторизації.
Ідеали і фактори¶
У цьому розділі ми збудуємо і розглянемо основні обчислення із ідеалами та фактор-кільцями.
Ідеали¶
Після побудови кільця і вибору списку генерувальних елементів ідеал, генерований цим списком, будується за допомогою оператору *.
sage: R.<x> = PolynomialRing(QQ)
sage: I = [2*x^2 + 8*x - 10, 10*x - 10]*R; I
Principal ideal (x - 1) of Univariate Polynomial Ring in x over Rational Field
sage: J = [ x^2 + 1, x^3 + x ]*R; J
Principal ideal (x^2 + 1) of Univariate Polynomial Ring in x over Rational Field
sage: K = [ x^2 + 1, x - 2]*R; K
Principal ideal (1) of Univariate Polynomial Ring in x over Rational Field
Sage автоматично скорочує набір генераторів. У цьому можна переконатись за допомогою методу gens(), що повертає список генерувальних елементів ідеалу.
sage: I.gens()
(x - 1,)
sage: J.gens()
(x^2 + 1,)
sage: K.gens()
(1,)
Належність до ідеалу можна визначити за допомогою умовного оператора in.
sage: R(x-1) in I
True
sage: R(x) in I
False
sage: R(2) in J
False
sage: R(2) in K
True
Деякі властивості ідеалу можна визначити за допомогою відповідних методів is_. Наприклад, для визначення, чи є ідеали простими, головними чи ідемпотентними, треба ввести наступні команди:
sage: J.is_prime()
True
sage: K.is_prime()
False
sage: I.is_idempotent()
False
sage: K.is_principal()
True
Ідеали у багатоваріантному поліноміальному кільці¶
Для побудови ідеалу у мультиваріантному поліноміальному кільці спочатку треба сконструювати поліноміальне кільце із упорядкуванням членів та набір поліномів, що генерують цей ідеал.
sage: R.<x,y,z> = PolynomialRing(QQ,3,order='lex')
sage: p = -1/2*x - y*z - y + 8*z^2
sage: q = -32*x + 2869*y - z^2 - 1
Ідеал будуємо так само, як і раніше.
sage: I = [p,q]*R
sage: I
Ideal (-1/2*x - y*z - y + 8*z^2, -32*x + 2869*y - z^2 - 1) of Multivariate Polynomial Ring in x, y, z over Rational Field
Якщо кільце є багатоваріантний поліном. можна обчислити спеціальний набір генераторів для I, який називається базисом_грёбнера.
sage: I.groebner_basis()
[x - 2869/32*y + 1/32*z^2 + 1/32, y*z + 2933/64*y - 513/64*z^2 - 1/64]
Є різні алгоритми для знаходження базису Грёбнера. Змінити алгоритм можна, додаючи додаткові аргументи до команди groebner_basis(). Наступна команда будує базис Грёбнера за допомогою алгоритму Бухбергера із зображенням проміжних результатів. Така функція досить корисна для навчання.
sage: set_verbose(3)
sage: I.groebner_basis('toy:buchberger')
(-32*x + 2869*y - z^2 - 1, -1/2*x - y*z - y + 8*z^2) => -2*y*z - 2933/32*y + 513/32*z^2 + 1/32
G: set([-2*y*z - 2933/32*y + 513/32*z^2 + 1/32, -1/2*x - y*z - y + 8*z^2, -32*x + 2869*y - z^2 - 1])
(-1/2*x - y*z - y + 8*z^2, -32*x + 2869*y - z^2 - 1) => 0
G: set([-2*y*z - 2933/32*y + 513/32*z^2 + 1/32, -1/2*x - y*z - y + 8*z^2, -32*x + 2869*y - z^2 - 1])
(-1/2*x - y*z - y + 8*z^2, -2*y*z - 2933/32*y + 513/32*z^2 + 1/32) => 0
G: set([-2*y*z - 2933/32*y + 513/32*z^2 + 1/32, -1/2*x - y*z - y + 8*z^2, -32*x + 2869*y - z^2 - 1])
(-32*x + 2869*y - z^2 - 1, -2*y*z - 2933/32*y + 513/32*z^2 + 1/32) => 0
G: set([-2*y*z - 2933/32*y + 513/32*z^2 + 1/32, -1/2*x - y*z - y + 8*z^2, -32*x + 2869*y - z^2 - 1])
3 reductions to zero.
[x + 2*y*z + 2*y - 16*z^2, x - 2869/32*y + 1/32*z^2 + 1/32, y*z + 2933/64*y - 513/64*z^2 - 1/64]
Можна обчислити різні ідеали приведення за допомогою методу elimination_ideal().
sage: I.elimination_ideal([x])
Ideal (64*y*z + 2933*y - 513*z^2 - 1) of Multivariate Polynomial Ring in x, y, z over Rational Field
sage: I.elimination_ideal([x,y])
Ideal (0) of Multivariate Polynomial Ring in x, y, z over Rational Field
sage: I.elimination_ideal([x,z])
Ideal (0) of Multivariate Polynomial Ring in x, y, z over Rational Field
sage: I.elimination_ideal([x])
Ideal (64*y*z + 2933*y - 513*z^2 - 1) of Multivariate Polynomial Ring in x, y, z over Rational Field
sage: I.elimination_ideal([y])
Ideal (64*x*z + 2933*x + 2*z^3 - 45902*z^2 + 2*z + 2) of Multivariate Polynomial Ring in x, y, z over Rational Field
sage: I.elimination_ideal([z])
Ideal (263169*x^2 + 128*x*y^2 - 47095452*x*y + 16416*x - 11476*y^3 + 2106993608*y^2 - 1468864*y + 256) of Multivariate Polynomial Ring in x, y, z over Rational Field
sage: I.elimination_ideal([x,y])
Ideal (0) of Multivariate Polynomial Ring in x, y, z over Rational Field
Фактор-кільця¶
Для побудови фактор-кільця для кільця з ідеалом треба використати метод quotient().
sage: R = ZZ
sage: I = R*[5]
sage: I
Principal ideal (5) of Integer Ring
sage: Q = R.quotient(I)
sage: Q
Ring of integers modulo 5
Для виконання арифметичних дій на фактор-кільці спочатку треба зробити приведення типу елементів до цього всесвіту. Більше про те, для чого це робиться - див. розділ Універсуми та приведення типів.
sage: Q(10)
0
sage: Q(12)
2
sage: Q(10) + Q(12)
2
sage: Q(10 + 12)
2
Добра практика при роботі із фактор-групами поліноміальних кілець полягає у присвоєнні нових імен невизначеним змінним.
sage: R.<x> = PolynomialRing(ZZ)
sage: parent(x)
Univariate Polynomial Ring in x over Integer Ring
sage: I = R.ideal(x^2 + 1)
sage: Q.<a> = R.quotient(I)
sage: parent(a)
Univariate Quotient Polynomial Ring in a over Integer Ring with modulus x^2 + 1
sage: a^2
-1
sage: x^2
x^2
Завдяки цьому виконувати арифметичні дії у цій фактор-групі можна без виконання явного приведення типів.
sage: 15*a^2 + 20*a + 1
20*a - 14
sage: (15 + a)*(14 - a)
-a + 211
Властивості кілець¶
Тепер можна перевірити деякі властивості щойно побудованих кілець. Наприклад, перевіримо, чи кільце є цілочисельною областю чи полем. Для цього використаємо відповідно методи is_integral_domain() та is_field().
sage: QQ.is_field()
True
sage: ZZ.is_integral_domain()
True
sage: ZZ.is_field()
False
sage: R=Integers(15)
sage: R.is_integral_domain()
False
sage: S=Integers(17)
sage: S.is_field()
True
Часто наявність цих властивостей встановлюється автоматично, оскільки вони вже є закладеними у визначення кільця, і, відповідно, немає потреби у їх динамічній перевірці.
Для отримання вичерпного списку вбудованих властивостей кільця можна використати вбудовану функцію автодоповнення Sage. Наприклад, щоб вивести всі властивості, які визначаються для раціональних чисел, введемо текст QQ.is і натиснемо клавішу табуляції. Ми отримаємо список усіх властивостей, які можна обчислити.
sage: QQ.is[TAB]
QQ.is_absolute QQ.is_finite QQ.is_ring
QQ.is_atomic_repr QQ.is_integral_domain QQ.is_subring
QQ.is_commutative QQ.is_integrally_closed QQ.is_zero
QQ.is_exact QQ.is_noetherian
QQ.is_field QQ.is_prime_field
Обчислити характеристику кільця можна за допомогою методу characteristic().
sage: QQ.characteristic()
0
sage: R=Integers(43)
sage: R.characteristic()
43
sage: F.<a> = FiniteField(9)
sage: F.characteristic()
3
sage: ZZ.characteristic()
0
Міні-розділ: Алгоритм ділення для поліномів із декількома змінними¶
У цьому розділі ми використаємо Sage для побудови алгоритму ділення для поліномів від декількох змінних. Зокрема, для даного поліному 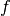 (подільне) та послідовності поліномів
(подільне) та послідовності поліномів 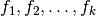 (дільники) треба визначити послідовність коефіцієнтів
(дільники) треба визначити послідовність коефіцієнтів 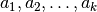 та залишковий поліном
та залишковий поліном  , такі, що
, такі, що

причому жоден з членів  не ділиться жодним з провідних членів
не ділиться жодним з провідних членів 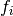 .
.
Перш за все потрібно побудувати базисне поле для поліноміального кільця та визначити, скільки змінних має містити поліноміальне кільце. У нашому випадку визначимо поліноміальне кільце із двома змінними на скінченному полі 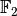 .
.
sage: K = GF(2)
sage: n = 2
Тепер побудуємо поліноміальне кільце.
sage: P.<x,y> = PolynomialRing(F,2,order="lex")
Оскільки ми працюємо із більш ніж однією змінною, необхідно вказати Sage спосіб упорядкування членів; у нашому випадку ми вибрали словниковий спосіб упорядкування. Спосіб, що вибирається за замовчуванням - ступенево-обернено-словниковий, тобто спочатку для визначення порядку мономів визначається повний ступінь, після чого для розбивання зв’язків використовується обернено-словникове упорядкування. Іншими можливими способами упорядкування мономів є deglex (ступенево-словниковий), або блочне впорядкування із заданням команди TermOrder(). Подальші відомості про способи впорядкування мономів див. у Wikipedia або MathWorld, або у підручнику [Cox2007] .
| [Cox2007] | Cox, David and Little, John and O’Shea, Donald, Ideals, varieties, and algorithms. Springer 2007 |
Тепер почнемо будувати алгоритм ділення. Спочатку визначимо функцію, яка встановлює, чи два мономи ділять один другий.
def does_divide(m1,m2):
for c in (vector(ZZ, m1.degrees()) - vector(ZZ,m2.degrees())):
if c < 0:
return False
return True
Тепер визначимо послідовність поліномів, що будуть використовуватись для зведення нашого подільного.
sage: F = [x^2 + x, y^2 + y]
Тепер визначимо поліном, який будемо приводити.
sage: f = x^3* y^2
Визначимо список факторів і решту і ініціалізуємо їх зі значеннями  .
.
sage: A = [P(0) for i in range(0,len(F)) ]
sage: r = P(0)
Оскільки f змінюється під час виконання алгоритму, зробимо його копію із тим, щоб зберегти первинне значення 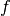 для наступної перевірки алгоритму.
для наступної перевірки алгоритму.
sage: p = f
Тепер можна задати головний цикл алгоритму.
while p != P(0):
i = 0
div_occurred = False
while (i < len(F) and div_occurred == False):
print A,p,r
if does_divide(p.lm(), F[i]):
q = P(p.lm()/F[i].lm())
A[i] = A[i] + q
p = p - q*F[i]
div_occurred = True
else:
i = i + 1
if div_occurred == False:
r = r + p.lm()
p = p - p.lm()
print A, p, r
Поля¶
Поля чисел¶
Поле чисел створюється визначенням незвідного поліному та імені для кореня цього поліному. Можна використати невизначену змінну 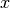 , вже визначену у Sage. Також можна створити поліноміальне кільце над раціональними числами та використати невизначену змінну для цього кільця.
, вже визначену у Sage. Також можна створити поліноміальне кільце над раціональними числами та використати невизначену змінну для цього кільця.
sage: P.<t> = PolynomialRing(QQ)
sage: K.<a> = NumberField(t^3-2)
sage: K
Number Field in a with defining polynomial t^3 - 2
sage: K.polynomial()
t^3 - 2
“Випадковий елемент” можна сконструювати, створивши елемент ступені не вище 2 (на одиницю менше, ніж ступінь визначального поліному). Для побудови числівника або знаменника можна використати опції num_bound() або dem_bound().
sage: K.random_element()
-5/14*a^2 + a - 3
sage: K.random_element()
-2*a
sage: K.random_element(num_bound= 2)
-a^2 + 1
Кожний ірраціональний елемент буде мати мінімальний поліном ступеню 3.
sage: a.minpoly()
x^3 - 2
sage: (a^2-3*a).minpoly()
x^3 + 18*x + 50
Перевіримо ізоморфізм полів.
sage: K.<a>= NumberField(t^3-2)
sage: L.<b> = NumberField(t^3-6*t-6)
sage: K.is_isomorphic(L)
True
Кількість дійсних вкладень та пар комплексних вкладень дається сигнатурою поля. Можна також побудувати вкладення у дійсне поле RR() , або комплексне поле CC().
sage: K.signature()
(1, 1)
sage: K.real_embeddings()
[
Ring morphism:
From: Number Field in a with defining polynomial t^3 - 2
To: Real Field with 53 bits of precision
Defn: a |--> 1.25992104989487
]
sage: K.complex_embeddings()
[
Ring morphism:
From: Number Field in a with defining polynomial t^3 - 2
To: Complex Field with 53 bits of precision
Defn: a |--> -0.629960524947437 - 1.09112363597172*I,
Ring morphism:
From: Number Field in a with defining polynomial t^3 - 2
To: Complex Field with 53 bits of precision
Defn: a |--> -0.629960524947437 + 1.09112363597172*I,
Ring morphism:
From: Number Field in a with defining polynomial t^3 - 2
To: Complex Field with 53 bits of precision
Defn: a |--> 1.25992104989487
]
sage: phi1, phi2, phi3 = K.complex_embeddings()
sage: phi1(a)
-0.629960524947437 - 1.09112363597172*I
sage: phi2(a)
-0.629960524947437 + 1.09112363597172*I
sage: phi3(a^2+3*a+5)
10.3671642016528
Метод Galois group() дозволяє обчислити групу Галуа від замикання Галуа, а не від самого поля. Якщо група Галуа не є циклічною, як у другому прикладі, необхідно назвати один з генераторів. Генератори можна також вивести як показано нижче.
sage: G = L.galois_group()
sage: G.gens()
[(1,2,3)]
sage: H.<g>= K.galois_group()
sage: H.gens()
[(1,2)(3,4)(5,6), (1,4,6)(2,5,3)]
sage: H.0
(1,2)(3,4)(5,6)
sage: H.1
(1,4,6)(2,5,3)
Замикання Галуа K.
sage: L.<b> = K.galois_closure()
sage: L
Number Field in b with defining polynomial t^6 + 40*t^3 + 1372
Розширення полів¶
Побудуємо розширення полів. Це можна зробити кількома різними способами. Методи absolute_() відносяться до простого поля  , а методи
, а методи relative_() - до побудованого розширення поля, яке може бути по відношенню до деякого проміжного поля.
sage: P.<t> = PolynomialRing(QQ)
sage: K.<a> = NumberField(t^3-2)
sage: L.<b> = NumberField(t^3-a)
sage: L.relative_degree(); L.relative_polynomial()
3
t^3 - a
sage: L.base_field()
Number Field in a with defining polynomial t^3 - 2
sage: L.absolute_degree(); L.absolute_polynomial()
9
x^9 - 2
sage: L.gens()
(b, a)
Також можна побудувати зіставне поле з декількох полів, визначене списком поліномів над раціональними числами. Для кожного поліному треба вказати корінь. У наступному прикладі Sage створює послідовність з 3 полів, починаючи з правого елементу списку.
sage: M.<a,b,c> = NumberField([t^3-2, t^2-3, t^3-5])
sage: M
Number Field in a with defining polynomial t^3 - 2 over its base field
sage: M.relative_degree()
3
sage: M.absolute_degree()
18
sage: d = M.absolute_generator(); d
a - b + c
sage: d.minpoly()
x^3 + (3*b - 3*c)*x^2 + (-6*c*b + 3*c^2 + 9)*x + (3*c^2 + 3)*b - 9*c - 7
sage: d.absolute_minpoly()
x^18 - 27*x^16 - 42*x^15 + 324*x^14 + 378*x^13 - 2073*x^12 + 1134*x^11 - 6588*x^10 - 23870*x^9 + 88695*x^8 + 79002*x^7 - 147369*x^6 - 1454922*x^5 + 431190*x^4 + 164892*x^3 + 2486700*x^2 - 1271592*x + 579268
У наступному прикладі будується замикання Галуа K(), де треба задати корені одиниці. Генератор L() - це об’єкт, який обчислює Sage, і він може містити мінімальний поліном складної структури, як видно тут. Ми знаємо, що L() містить кубічні корені одиниці, тому перевіримо це.
sage: K.<a> = NumberField(t^3-2)
sage: L.<b> = K.galois_closure()
sage: b.minpoly()
x^6 + 40*x^3 + 1372
sage: units= L.roots_of_unity(); units
[1/36*b^3 + 19/18, 1/36*b^3 + 1/18, -1, -1/36*b^3 - 19/18, -1/36*b^3 - 1/18, 1]
sage: len(units)
6
sage: [u^3 for u in units]
[-1, 1, -1, 1, -1, 1]
Спеціальні чисельні поля¶
Є два класи чисельних полів із особливими властивостями, які можна збудувати безпосередньо. Для розширення квадратичного поля слід просто вказати вільне від квадратів ціле число.
sage: F.<a> = QuadraticField(17)
sage: a^2
17
sage: (7*a-3).minpoly()
x^2 + 6*x - 824
Циклотомічне поле будуємо завданням його примітивних коренів одиниці.
CyclotomicField()
QuadraticField()
Скінченні поля¶
У попередньому розділі ми будували кільця цілих чисел за модулем 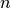 . Ми знаємо, що якщо
. Ми знаємо, що якщо 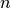 є простим числом, то кільце
є простим числом, то кільце 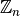 є полем. У Sage можна побудувати той самий об’єкт як кільце або як поле.
є полем. У Sage можна побудувати той самий об’єкт як кільце або як поле.
sage: R = Integers(7)
sage: F7 = GF(7)
sage: R, F7
(Ring of integers modulo 7, Finite Field of size 7)
Для побудови цього об’єкту, щоб скористатись можливостями цієї додаткової структури, краще використати команду GF() (або, що те ж саме, FiniteField()). Як і для кілець за модулем, для виконання арифметичних дій треба виконати перетворення типу цілих чисел до поля.
sage: F7(4 + 3)
0
sage: F7(2*3)
6
sage: F7(3*7)
0
sage: F7(3/2)
5
Можна використати Sage для створення скінченного поля. Нагадаємо, що скінченне поле завжди має порядок 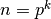 , де
, де 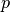 - просте число. Для побудови поля порядку
- просте число. Для побудови поля порядку 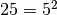 вводимо наступну команду
вводимо наступну команду
sage: F25.<a> = GF(25)
Пригадаємо, що скінченне поле порядку 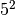 можна розглядати як розширення
можна розглядати як розширення 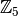 із використанням коренів поліному ступеню
із використанням коренів поліному ступеню 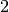 . Вказаний параметр
. Вказаний параметр a - це корінь поліному. Для побудови такого розширення можна використати різні поліноми, і Sage у кожному випадку вибирає якійсь один з них. Подивитись, який обрано поліном, можна за допомогою метода з інтуїтивною назвою polynomial().
sage: p = F25.polynomial();
sage: p
a^2 + 4*a + 2
Можна перевірити, що a дійсно є коренем цього поліному.
sage: a^2 + 4*a + 2
0
Відмітимо, що a вже існує в структурі поля, тому для виконання арифметичних дій із a спеціальне перетворення типів непотрібне.
sage: parent(a)
Finite Field in a of size 5^2
sage: a^2
a + 3
sage: a*(a^2 + 1)
3
Але якщо використовуються тільки цілі числа, необхідно зробити перетворення типу для арифметичних дій до поля.
sage: 3+4
7
sage: parent(3+4)
Integer Ring
sage: F25(3 + 4)
2
sage: parent(F25(3+4))
Finite Field in a of size 5^2
Іноді є потреба вказати поліном, що використовується для розширення, у такому випадку слід додати опцію модуль до конструктора поля.
sage: F25.<a> = GF(25, modulus=x^2 + x + 1)
sage: a^2 + a + 1
0
sage: a^2
4*a + 4
Пам’ятаймо, що модуль має бути поліномом, незвідним щодо ![\mathbb{F}_{5}[x]](_images/math/c472392dec9847eeab3151a273bb6d6301350233.png) . У багатьох випадках проте нам треба мати модуль не тільки незвідний, але й примітивний. Далі ми побудуємо всі примітивні поліноми ступеня
. У багатьох випадках проте нам треба мати модуль не тільки незвідний, але й примітивний. Далі ми побудуємо всі примітивні поліноми ступеня 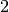 . У наступному прикладі використовуються Поліномінальні кільця та Згортання списків (цикли у списках). У першу чергу сконструюємо список усіх нормованих (зведених) поліномів над
. У наступному прикладі використовуються Поліномінальні кільця та Згортання списків (цикли у списках). У першу чергу сконструюємо список усіх нормованих (зведених) поліномів над 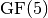
sage: F5 = GF(5)
sage: P.<x> = PolynomialRing(F, 'x')
sage: AP = [ a0 + a1*x + a2*x^2 for (a0,a1) in F^3]
sage: AP
[x^2, x^2 + 1, x^2 + 2, x^2 + 3, x^2 + 4, x^2 + x, x^2 + x + 1, x^2 + x + 2, x^2 + x + 3, x^2 + x + 4, x^2 + 2*x, x^2 + 2*x + 1, x^2 + 2*x + 2, x^2 + 2*x + 3, x^2 + 2*x + 4, x^2 + 3*x, x^2 + 3*x + 1, x^2 + 3*x + 2, x^2 + 3*x + 3, x^2 + 3*x + 4, x^2 + 4*x, x^2 + 4*x + 1, x^2 + 4*x + 2, x^2 + 4*x + 3, x^2 + 4*x + 4]
Далі ми відфільтровуємо зі списку примітивні поліноми.
sage: PR = [ p for p in AP if p.is_primitive() ]
sage: PR
[x^2 + x + 2, x^2 + 2*x + 3, x^2 + 3*x + 3, x^2 + 4*x + 2]
Якщо треба отримати всі незвідні поліноми, можна просто дещо змінити останню команду.
sage: IR = [ p for p in AP if p.is_irreducible() ]
sage: IR
[x^2 + 2, x^2 + 3, x^2 + x + 1, x^2 + x + 2, x^2 + 2*x + 3, x^2 + 2*x + 4, x^2 + 3*x + 3, x^2 + 3*x + 4, x^2 + 4*x + 1, x^2 + 4*x + 2]
Відмітимо, що цей код працює тільки якщо поліноми задано на скінченних кільцях або полях.
Вправи
Обчислити список усіх примітивних поліномів ступеня 3 над
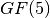 .
.Обчислити кількість примітивних елементів у
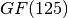 .
.Поясніть співвідношення між кількістю примітивних поліномів та кількістю примітивних елементів у цих вправах.
Функціональні поля¶
Теорія кодування¶
Лінійні коди¶
Лінійний код є скінченновимірний векторний простір, який зазвичай визначають над скінченним полем. Для побудови лінійного коду у Sage спочатку треба визначити скінченне поле та матрицю над цим полем, ранг якої визначатиме цей векторний простір.
sage: F = GF(2)
sage: G = matrix(F, [(0,1,0,1,0),(0,1,1,1,0),(0,0,1,0,1),(0,1,0,0,1)]); G
[0 1 0 1 0]
[0 1 1 1 0]
[0 0 1 0 1]
[0 1 0 0 1]
Сам код будуємо за допомогою команди LinearCode().
sage: C = LinearCode(G); C
Linear code of length 5, dimension 4 over Finite Field of size 2
Хоча довжина та розмірність коду відображені в описі об’єкту, ці параметри можна за потреби отримати за допомогою методів length() та dimension() коду.
sage: C.length()
5
sage: C.dimension()
4
Для двох слів коду можна обчислити їхню Вагу Хеммінга та відстань за допомогою функції hamming_weight().
sage: w1 = vector(F, (0,1,0,1,0)); w1
(0, 1, 0, 1, 0)
sage: hamming_weight(w1)
2
sage: w2 = vector(F, (0,1,1,0,1)); w2
(0, 1, 1, 0, 1)
sage: hamming_weight(w2)
3
sage: hamming_weight(w1 - w2)
3
Мінімальну відстань C можна обчислити методом minimum_distance().
sage: C.minimum_distance()
1
Також у Sage можна порахувати розподіл ваг для коду.
sage: C.weight_distribution()
[1, 4, 6, 4, 1, 0]
Значення під індексом i у списку, починаючи з нуля до довжини коду - це кількість слів коду із цією вагою.
Із розподілом ваги пов’язаний поліном вагового енумератора, який можна отримати за допомогою методу weight_enumerator() коду.
sage: C.weight_enumerator()
x^5 + 4*x^4*y + 6*x^3*y^2 + 4*x^2*y^3 + x*y^4
Генерувальна та перевірочна матриці обчислюються методами gen_mat() та check_mat().
sage: C.gen_mat()
[0 1 0 1 0]
[0 1 1 1 0]
[0 0 1 0 1]
[0 1 0 0 1]
sage: C.check_mat()
[1 0 0 0 0]
Систематичну форму генерувальної матриці отримуємо за допомогою gen_mat_systematic().
sage: C.gen_mat_systematic()
[0 1 0 0 0]
[0 0 1 0 0]
[0 0 0 1 0]
[0 0 0 0 1]
Sage може також виконати операції розширення та перфорації коду. Розширений код обчислюється наступним чином:
sage: Cx = C.extended_code(); Cx
Linear code of length 6, dimension 4 over Finite Field of size 2
sage: Cx.gen_mat()
[0 1 0 1 0 0]
[0 1 1 1 0 1]
[0 0 1 0 1 0]
[0 1 0 0 1 0]
sage: Cx.check_mat()
[1 0 0 0 0 0]
[0 1 1 1 1 1]
Перфорований код можна дістати, подаючи на вхід методу punctured() коду список координат для видалення. Наступні команди конструюють код із видаленням першої та третьої координати з кожного слова коду у C. Зауважимо, що на відміну від векторів, списків і матриць перша колонка при перфоруванні коду зазначається під номером 1, а не 0:
sage: Cp = C.punctured([1,3]); Cp
Linear code of length 3, dimension 2 over Finite Field of size 2
sage: Cp.gen_mat()
[0 1 0]
[0 0 1]
sage: Cp.check_mat()
[1 0 0]
У Sage можна також обчислити дуальний об’єкт до C.
sage: Cd = C.dual_code(); Cd
Linear code of length 5, dimension 1 over Finite Field of size 2
sage: Cd.gen_mat()
[1 0 0 0 0]
sage: Cd.check_mat()
[0 1 0 0 0]
[0 0 1 0 0]
[0 0 0 1 0]
[0 0 0 0 1]
І на кінець, Sage також декодує отримані вектори. У наступному прикладі моделюється комунікаційний канал. Ми починаємо із кодового слова, вводимо похибку і потім коригуємо цю похибку декодуванням отриманої відомості.
sage: wrd = vector(F,(0,0,0,0,1))
sage: err = vector(F,(0,0,1,0,0))
sage: msg = wrd + err; msg
(0, 0, 1, 0, 1)
sage: C.decode(msg)
(0, 0, 0, 0, 1)
sage: C.decode(msg) == wrd
True
Відмітимо, що оскільки цей код має мінімальну довжину 1, у такому декодуванні не завжди можна отримати очікуване слово коду,
Тут подано тільки деякі з команд, наявні у Sage для обчислення та обробки лінійних кодів. Більше інформації можна знайти на наступних сторінках:
Циклічні коди¶
Для побудови циклічного коду довжини  на
на  необхідно задати генерувальний поліном, який може бути будь-яким незвідним фактором
необхідно задати генерувальний поліном, який може бути будь-яким незвідним фактором  . Список незвідних факторів можна отримати за допомогою команди
. Список незвідних факторів можна отримати за допомогою команди factor().
sage: P.<x> = PolynomialRing(GF(2),'x')
sage: factor(x^3 -1 )
(x + 1) * (x^2 + x + 1)
З виводу можна побачити, що нетривіальні генерувальні поліноми можна задати двома способами. За допомогою наступних команд будується код, генерований 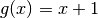 .
.
sage: g = x + 1
sage: C = CyclicCode(3,g)
sage: C.list()
[(0, 0, 0), (1, 0, 1), (0, 1, 1), (1, 1, 0)]
Циклічні коди є особливим типом лінійних кодів. Тому всі команди, розглянуті у попередньому розділі, будуть працювати подібно. Наприклад, генерувальну матрицю у стандартній та систематичній формах можна отримати наступним чином:
sage: G = C.gen_mat(); G
[1 1 0]
[0 1 1]
sage: Gs = C.gen_mat_systematic(); Gs
[1 0 1]
[0 1 1]
Щоби переконатись, що це саме генерувальна матриця, і повторити навички роботи із матрицями і векторами, перевіримо, чи образ  покриває код.
покриває код.
sage: vector(GF(2),[0,0])*G
(0,0,0)
sage: vector(GF(2),[1,0])*G
(1, 1, 0)
sage: vector(GF(2),[1,1])*G
(1, 0, 1)
sage: vector(GF(2),[0,1])*G
(0, 1, 1)
За допомогою Sage можна обчислити матрицю перевірки парності від  , використовуючи метод коду
, використовуючи метод коду check_mat().
sage: H = C.check_mat()
[1 1 1]
Безпосередньо можна перевірити, що H - це перевірочна матриця для  .
.
sage: H*vector(GF(2),[0,1,1])
(0)
sage: H*vector(GF(2),[1,0,1])
(0)
sage: H*vector(GF(2),[1,0,0])
(1)
Також можна збудувати дуальний код та його генерувальну та перевірочну матриці.
sage: Cp = C.dual_code()
sage: Cp.gen_mat()
[1 1 1]
sage: Cp.check_mat()
[1 0 1]
[0 1 1]
Міні-розділ: факторизація 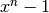 ¶
¶
Найменше поле, що містить 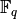 та корені
та корені 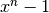 - це
- це 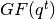 , де
, де 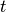 - це порядок
- це порядок 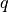 у
у  .
.
Фактори 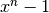 над
над 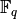 усі повинні мати ступінь, що ділить
усі повинні мати ступінь, що ділить 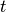 .
.
Почнемо із визначення 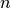 та
та 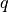 та побудови зовнішніх кілець.
та побудови зовнішніх кілець.
sage: n = 19
sage: q = 2
sage: F = GF(2)
sage: P.<x> = PolynomialRing(F, 'x')
Слід пам’ятати, що оскільки ми будуємо скінченне кільце, 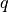 має бути або простим, або ступенем простого. Тепер обчислимо усі незвідні фактори
має бути або простим, або ступенем простого. Тепер обчислимо усі незвідні фактори 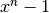 над
над 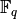 .
.
sage: A = factor(x^n-1); A
Тепер перевіримо встановлені раніше твердження щодо обчислених факторів. Порівняймо список, наведений вище із порядком  у
у 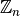 .
.
sage: Integers(19)(2).multiplicative_order()
Пам’ятаючи, що 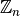 є кільцем, треба вказати, який тип впорядкування треба обчислити - адитивний або мультиплікативний.
є кільцем, треба вказати, який тип впорядкування треба обчислити - адитивний або мультиплікативний.
Тепер повторимо ці ж дії, але беручи 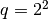 . Зміна тільки q не змінює базове поле і поліноміальне кільце. Тому треба перебудувати всі об’єкти, використовуючи новий параметр.
. Зміна тільки q не змінює базове поле і поліноміальне кільце. Тому треба перебудувати всі об’єкти, використовуючи новий параметр.
sage: q = 4
sage: F.<a> = GF(4,'a')
sage: P.<x> = PolynomialRing(F,'x')
Знову факторизуємо 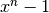 , але цього разу над непростим полем.
, але цього разу над непростим полем.
sage: A = factor(x^n-1); A
(x + 1) * (x^9 + a*x^8 + a*x^6 + a*x^5 + (a + 1)*x^4 + (a + 1)*x^3 + (a + 1)*x + 1) * (x^9 + (a + 1)*x^8 + (a + 1)*x^6 + (a + 1)*x^5 + a*x^4 + a*x^3 + a*x + 1)
Вправи
Повторіть ці дії для
.
Обчисліть порядок 2, 4. 8 mod 19. Що можна побачити?
Спробуйте різні значення n та різні поля.
Міні-розділ: ідемпотентні поліноми¶
Знайдемо ідемпотент, що є i-м коефіцієнтом 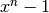 за модулем 1. Продовжуємо із
за модулем 1. Продовжуємо із 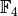 .
.
sage: F.<a> = GF(4, 'a')
sage: P.<x> = PolynomialRing(F, 'x')
Тепер створимо фактор-кільце.
sage: R.<y> = P.quotient(x^19 - 1)
sage: A = factor(x^19 - 1); A
(x + 1) * (x^9 + a*x^8 + a*x^6 + a*x^5 + (a + 1)*x^4 + (a + 1)*x^3 + (a + 1)*x + 1) * (x^9 + (a + 1)*x^8 + (a + 1)*x^6 + (a + 1)*x^5 + a*x^4 + a*x^3 + a*x + 1)
Оскільки команда factor() повертає список поліноміальних коефіцієнтів із їх кратностями, які нам наразі не потрібні, то відкинемо їх.
sage: A = [p[0] for p in A]
Ми тільки виберемо один з цих коефіцієнтів. Спробуйте самі вибрати інші коефіцієнти.
sage: p0 = A[2]
Знайдемо добуток усіх цих коефіцієнтів.
sage: ap = prod( [p for p in A if p != a])
x^10 + (a + 1)*x^9 + a*x^8 + a*x^7 + x^5 + (a + 1)*x^3 + (a + 1)*x^2 + a*x + 1
Тепер підрахуємо xgcd() на p0 та ap.
sage: d, s, t = xgcd(p0, ap)
Пригадаймо, що 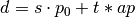 є розширеним найбільшим спільним дільником. Перевірте, що
є розширеним найбільшим спільним дільником. Перевірте, що 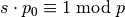 для усіх
для усіх  та
та 
sage: s*p0 % A[1]
1
sage: s*p0 % A[2]
0
sage: s*p0 % A[0]
1
Тепер перевірте, що 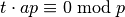 для
для 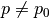 та
та 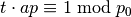 .
.
sage: t*ap % A[0]
0
sage: t*ap % A[1]
0
sage: t*ap % A[2]
1
Перевіримо, що обчислений поліном є ідемпотентним у ![F\left[x\right]/\left<x^n - 1 \right>](_images/math/58095574ef1f2d1928acb6a729ea46b4a930ff41.png) .
.
sage: f = R(bp*ap)
sage: f^2 == f
True
Перевіримо породжувальний поліном.
sage: gcd(b*p0, x^19-1)
x^9 + (a + 1)*x^8 + (a + 1)*x^6 + (a + 1)*x^5 + a*x^4 + a*x^3 + a*x + 1
sage: p0
x^9 + (a + 1)*x^8 + (a + 1)*x^6 + (a + 1)*x^5 + a*x^4 + a*x^3 + a*x + 1
Вправи
Знайдемо ідемпотентний елемент
для
та
та
.
Щодо поліномів, обернених до ідемпотентних, див. теорему 5 [MacWilliams1977] стор. 219
| [MacWilliams1977] | MacWilliams, F. J. and Sloane, N. J. A., The theory of error-correcting codes. North-Holland Publishing Co. 1977 |
Інші коди¶
Коди Хеммінга¶
Код Хеммінга є простий лінійний код, що здатний детектувати до двох помилок та виправляти будь-яку поодиноку помилку.
Почнемо із побудови двійкового коду Хеммінга із 3 перевірками парності.
sage: F = GF(2)
sage: C = HammingCode(3,F); C
Linear code of length 7, dimension 4 over Finite Field of size 2
Коди Хеммінга завжди мають довжину 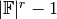 , де
, де  - це кількість перевірок парності і
- це кількість перевірок парності і 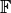 - скінченне поле, над яким задається код. Це пов’язано з тим, що колонки матриці перевірки парності містять всі ненульові елементи
- скінченне поле, над яким задається код. Це пов’язано з тим, що колонки матриці перевірки парності містять всі ненульові елементи 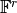 .
.
sage: C.check_mat()
[1 0 1 0 1 0 1]
[0 1 1 0 0 1 1]
[0 0 0 1 1 1 1]
Трійковий код Хеммінга будуємо завданням небінарного скінченного поля у якості основного поля. У наступному прикладі побудуємо трійковий код Хеммінга над 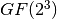 також з 3 перевірками парності.
також з 3 перевірками парності.
sage: C = HammingCode(3, F); C
Linear code of length 73, dimension 70 over Finite Field in a of size 2^3
Дивись також
Коди BHC¶
Коди BCH (БЧХ), або коди Боуза - Чоудхурі - Хоквінгема є спеціальним класом циклічних кодів із 3 обов’язковими параметрами  та одним опціональним
та одним опціональним 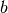 . Тут
. Тут 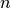 - це довжина слів коду,
- це довжина слів коду, 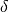 - параметр, що називають призначена відстань, а
- параметр, що називають призначена відстань, а 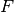 - скінченне поле порядку
- скінченне поле порядку 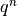 , де
, де 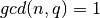 .
.
Якщо параметр 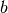 не задано, тоді використовується значення 0 за замовчуванням. Наприклад, будуємо код BCH довжини
не задано, тоді використовується значення 0 за замовчуванням. Наприклад, будуємо код BCH довжини 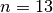 із
із  над
над 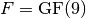 .
.
sage: F.<a> = GF(3^2,'a')
sage: C = BCHCode(13, 5, F)
sage: C
Linear code of length 13, dimension 6 over Finite Field in a of size 3^2
Обчислимо мінімальну відстань коду за допомогою його методу minimum_distance().
sage: C.minimum_distance()
6
Оскільки коди BHC є також лінійними, у Sage можна побудувати генерувальну та перевірочну матриці коду.
sage: C.gen_mat()
[2 2 1 2 0 0 1 1 0 0 0 0 0]
[0 2 2 1 2 0 0 1 1 0 0 0 0]
[0 0 2 2 1 2 0 0 1 1 0 0 0]
[0 0 0 2 2 1 2 0 0 1 1 0 0]
[0 0 0 0 2 2 1 2 0 0 1 1 0]
[0 0 0 0 0 2 2 1 2 0 0 1 1]
sage: C.check_mat()
[1 0 0 0 0 0 0 1 2 1 2 2 2]
[0 1 0 0 0 0 0 1 0 0 0 1 1]
[0 0 1 0 0 0 0 2 2 2 1 1 2]
[0 0 0 1 0 0 0 1 1 0 1 0 0]
[0 0 0 0 1 0 0 0 1 1 0 1 0]
[0 0 0 0 0 1 0 0 0 1 1 0 1]
[0 0 0 0 0 0 1 2 1 2 2 2 1]
Також можна обчислити його дуальний код.
sage: Cp = C.dual_code(); Cp
Linear code of length 13, dimension 7 over Finite Field in a of size 3^2
sage: Cp.gen_mat()
[1 0 0 0 0 0 0 1 2 1 2 2 2]
[0 1 0 0 0 0 0 1 0 0 0 1 1]
[0 0 1 0 0 0 0 2 2 2 1 1 2]
[0 0 0 1 0 0 0 1 1 0 1 0 0]
[0 0 0 0 1 0 0 0 1 1 0 1 0]
[0 0 0 0 0 1 0 0 0 1 1 0 1]
[0 0 0 0 0 0 1 2 1 2 2 2 1]
sage: Cp.check_mat()
[1 0 0 0 0 0 2 2 1 2 0 0 1]
[0 1 0 0 0 0 1 0 1 2 2 0 2]
[0 0 1 0 0 0 2 0 1 0 2 2 1]
[0 0 0 1 0 0 1 0 2 2 0 2 1]
[0 0 0 0 1 0 1 2 2 0 2 0 1]
[0 0 0 0 0 1 1 2 1 0 0 2 2]
Дивись також